Dependently Typed Activation Functions
Types for numbers within a range
Using dependent types, we can provide types that require a proof that some value is within a certain range. For example, in Idris1:
data Range : Ord n => n -> n -> Type where
MkRange :
Ord n =>
(x, a, b : n) ->
((x > a) && (x < b) = True) ->
Range a bEssentially, this snippet means “given two things a and
b and some third thing x, all orderable, and
given a proof that x > a and x < b, we
can construct a Range a b representing the fact that
x is within the range from a to
b”. If we don’t supply a valid proof, our code will fail to
typecheck.
For example, because 2 is between 1 and
3, if we call the MkRange constructor with
MkRange 2 1 3 Refl (where you can think of
Refl as a proof of equality), then we get a value of type
Range 1 3, with a 2 inside.
Of course, this means we can create a more-specific type with a limited range. For example, a range where all values must be Double and are limited to being greater than zero and less than one is totally valid:
data BetweenZeroAndOne : Type where
MkBetweenZeroAndOne :
(x : Double) ->
((x > 0.0) && (x < 1.0) = True) ->
BetweenZeroAndOneSimilarly to the above, doing
MkBetweenZeroAndOne 0.5 Refl works fine, and
MkBetweenZeroAndOne 2.5 Refl gives us this lovely type
error:
When checking an application of
constructor Main.MkBetweenZeroAndOne:
Type mismatch between
x = x (Type of Refl)
and
2.5 > 0.0 && Delay (2.5 < 1.0) = True (Expected type)
Specifically:
Type mismatch between
False
and
TrueActivation Functions
Let’s switch gears for a little bit. In machine learning, the neurons in our neural networks will have an “activation function”, a little bit of math that describes how much a neuron “activates” in response to its input, and whose derivative is relevant to things like learning speed.
One commonly-used activation function is ReLU (rectified linear unit). It’s defined by \(f(x) = \max(0, x)\), which is linear but capped-from-below at zero.2
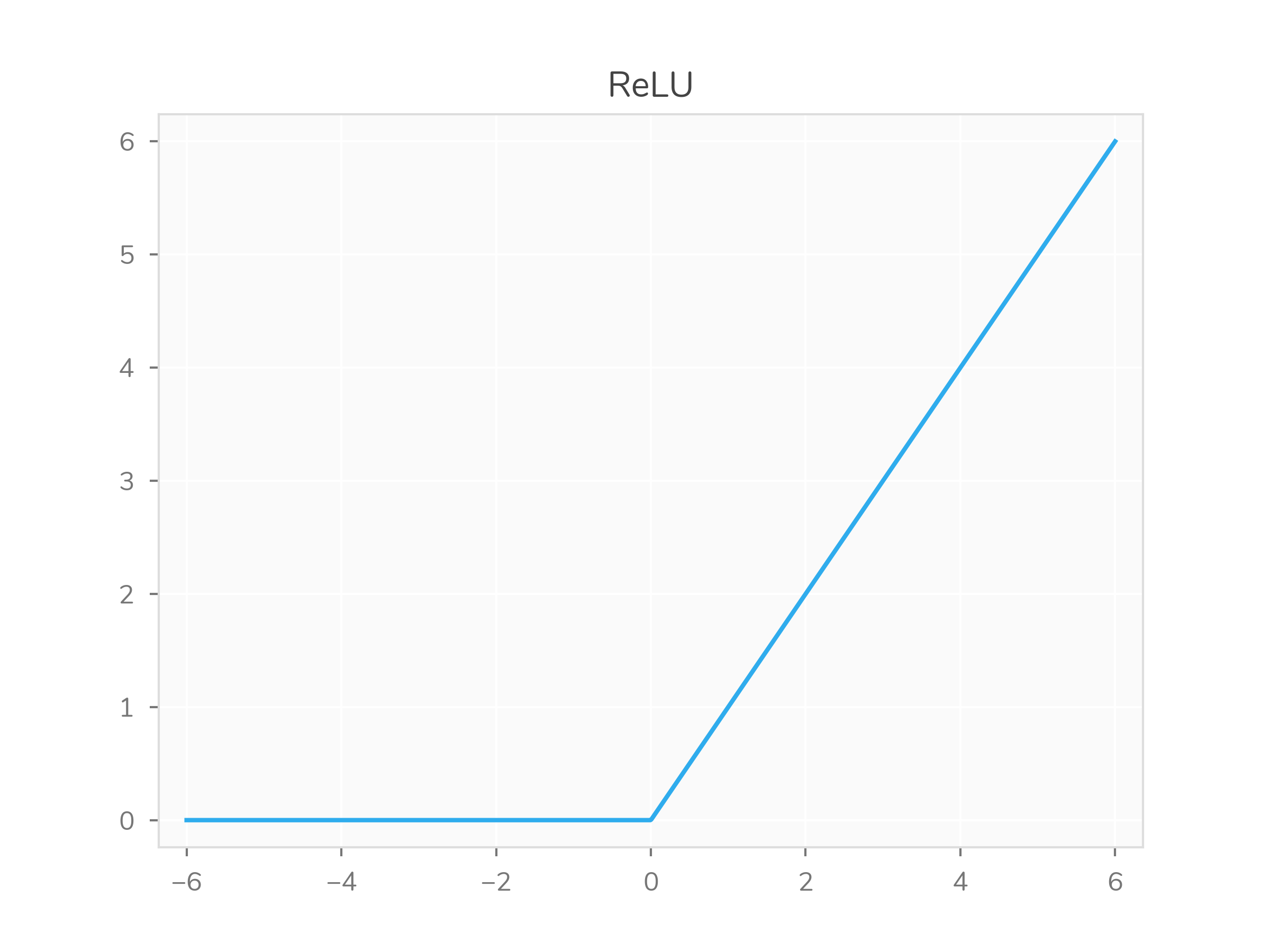
However, there are some properties of ReLU that aren’t what you want in all situations. For example, if your activation ever crosses into the constant-zero region, backpropagation becomes “stuck” and doesn’t update further. Also, ReLU is only really used in hidden layers. We often want output layers to be scaled to within some region.
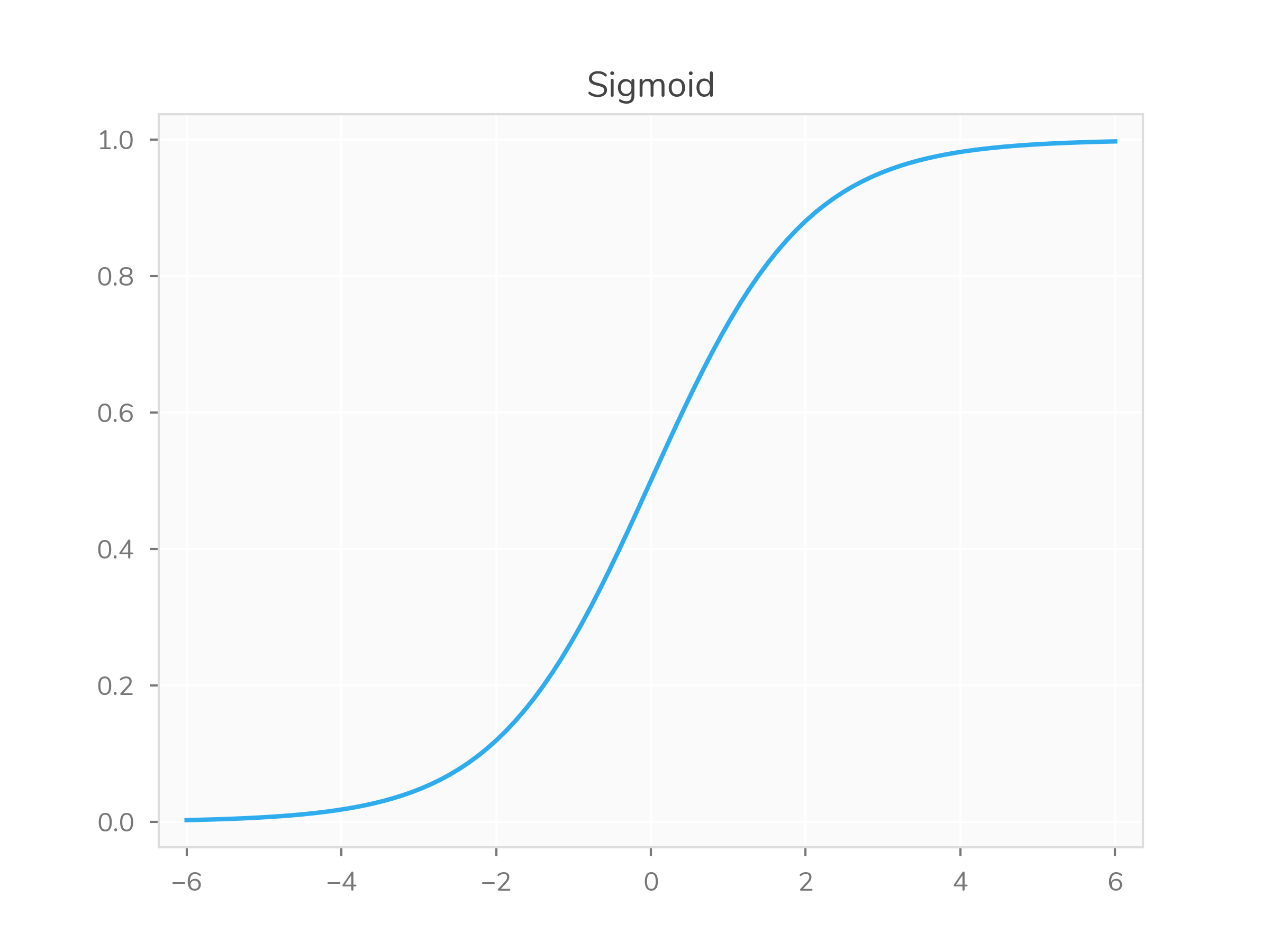
One activation function that has this kind of nicely-scaled output is
the sigmoid (an S-shaped curve): \(\frac{1}{1+e^{-x}}\). It produces values
between zero and one, which can easily be shown by showing \(\underset{x\rightarrow\infty}{\lim}
\frac{1}{1+e^{-x}} = 1\) and \(\underset{x\rightarrow -\infty}{\lim}
\frac{1}{1+e^{-x}} = 0\). (You’ve probably already connected the
dots to the fancy BetweenZeroAndOne type, but stay with
me.) It’s often used for binary classification problems, where the
classes can be represented as \(0\) or
\(1\).
Another similar activation function is \(\tanh(x)\), though its bounds stretch from \(-1\) to \(1\) and it has the nice property of being centered around \(0\).
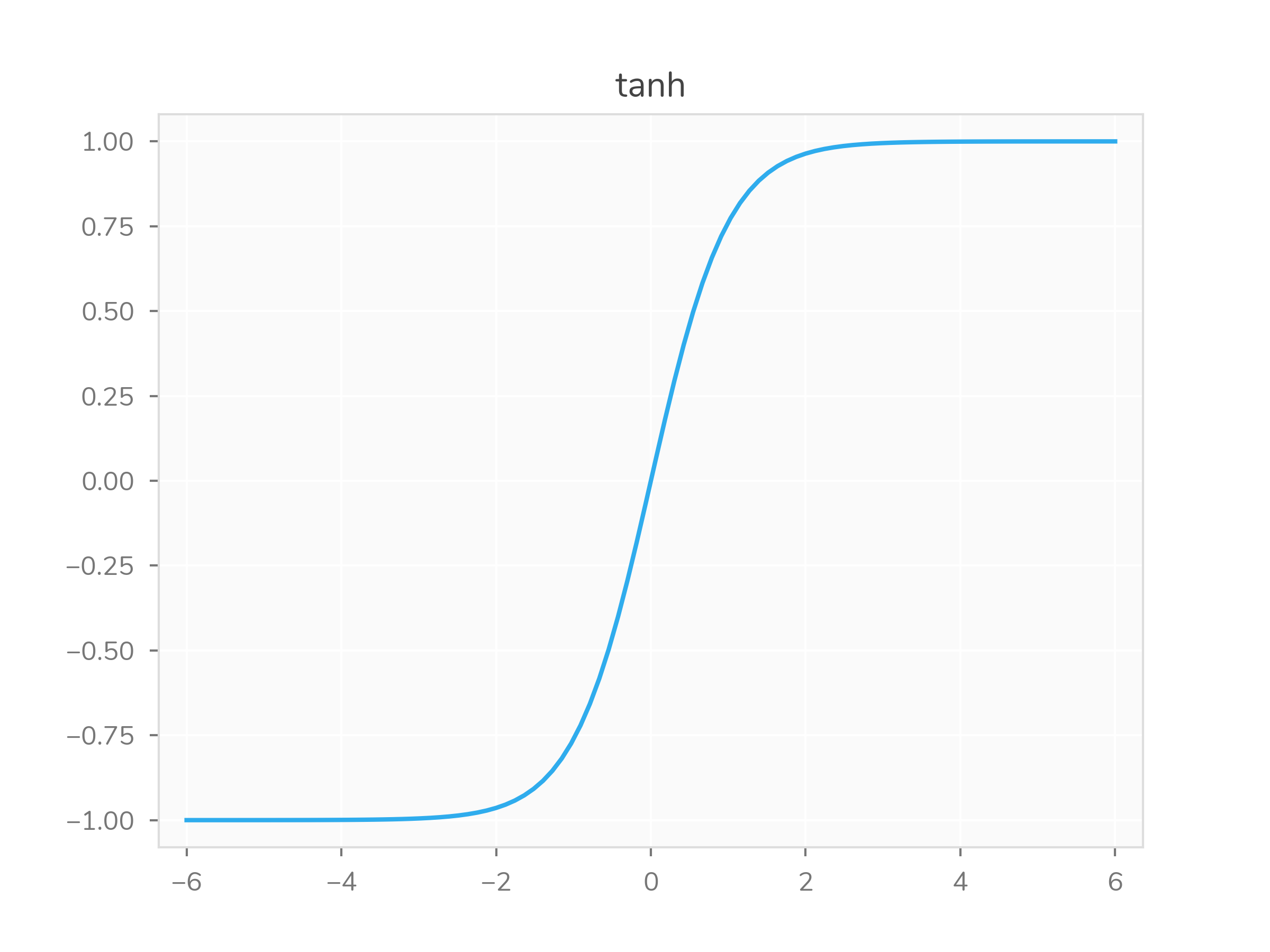
Note that these aren’t the only activation functions, or the only ones bounded between certain values, but they’re enough to make my point here.
Using types to maintain neural net properties
Finally, here’s the main idea: we could use dependent types to ensure our activation functions have certain properties, making our neural networks slightly easier to understand.
There are already fine examples of using dependent types in machine learning. For example, grenade is a Haskell library that uses heterogeneous type-level lists of neural network layers to ensure that the network has a valid shape.3
Neural network interpretability is a pretty hard problem. A phrase I’ve often heard about NNs is “black box”, meaning there’s no real way to peek inside and make sense of all the complexity. While providing activation function bounds, even for every neuron in the net, doesn’t give total assurance of good behavior, it at least places some bounds on what kinds of trickery the network can get up to.
Of course, sigmoid activation already has these kinds of bounds mathematically built in. Redundantly stating some property is small assurance. However, it’s fairly common to mess with neural net internals, including activation functions, in the process of tweaking the network towards better performance. Also, types are helpful for sharing. What if I want to give you some network, so you can play with it, but I still want to provide certain bounds on the kinds of things we can do to it? Types are a good way to encode this kind of thing, much better than easily-broken conventions. Finally, we might imagine parts of the network itself being learned. If a network is tweaking itself (or being tweaked by some other learner), it could be very helpful to have solid bounds on what kinds of tweaks are not allowed.
Proving other properties of activation functions
There’s one more thing I want to show: that this kind of
properties-checked-in-types coding can go beyond enforcing a simple
Range.
It’s hard to ensure the behavior of a function in code is “correct” at every single point. Say I gave you this function, without describing its internals:
f x = if x > 0.70 && x < 0.71 then 7000 else xIf you happened to never test values between \(0.70\) and \(0.71\), you might assume this function was better-behaved than it really is.
However, even without these kinds of analytical proofs of good function behavior, we can come up with good sanity checks in types, that prevent compilation if something is obviously wrong.
Recall how I declared that \(\tanh\)
was centered around zero, and that was a nice property. We can encode a
quick check on that kind of thing, by testing that \(f(-1)\) and \(f(1)\) are a negation of each other (we’ll
ignore floating point/numerical computation issues here). That is, we
want to express \(-f(-1) = f(1)\).
Instead of taking a lower and upper bound, like we did for
Range, we can take in the function itself, and test it at
\(-1\) and \(1\). We’ll use a function of type
Double -> Double for simplicity.
data ValuesNegatedAtPlusOrMinusOne :
(Double -> Double) -> Type where
MkValuesNegatedAtPlusOrMinusOne :
(f : Double -> Double) ->
(-f (-1.0) = f 1.0) ->
ValuesNegatedAtPlusOrMinusOne fNow of course, when we construct
MkValuesNegatedAtPlusOrMinusOne tanh Refl we get a value of
type ValuesNegatedAtPlusOrMinusOne tanh, showing that
tanh observes this property. And, if we try
MkValuesNegatedAtPlusOrMinusOne (+1) Refl we get a
beautiful type error:
(input):1:1-41:When checking an application of
constructor Main.MkValuesNegatedAtPlusOrMinusOne:
Type mismatch between
x = x (Type of Refl)
and
(-(\ARG => ARG + 1) -1.0) =
(\ARG => ARG + 1) 1.0 (Expected type)
Specifically:
Type mismatch between
-0.0
and
2.0You can read a bit more about some benefits and drawbacks of this kind of thing here: https://stackoverflow.com/questions/28426191/how-to-specify-a-number-range-as-a-type-in-idris↩︎
Ironically for a post about using better types to do machine learning, I ran into some trouble plotting ReLU which better types would have fixed immediately. See if you can spot what’s wrong with this Python code.
It produces a “staircase” like this:x = np.linspace(-6.0, 6.0, 1000) y = np.vectorize(lambda x: max(0, x))(x)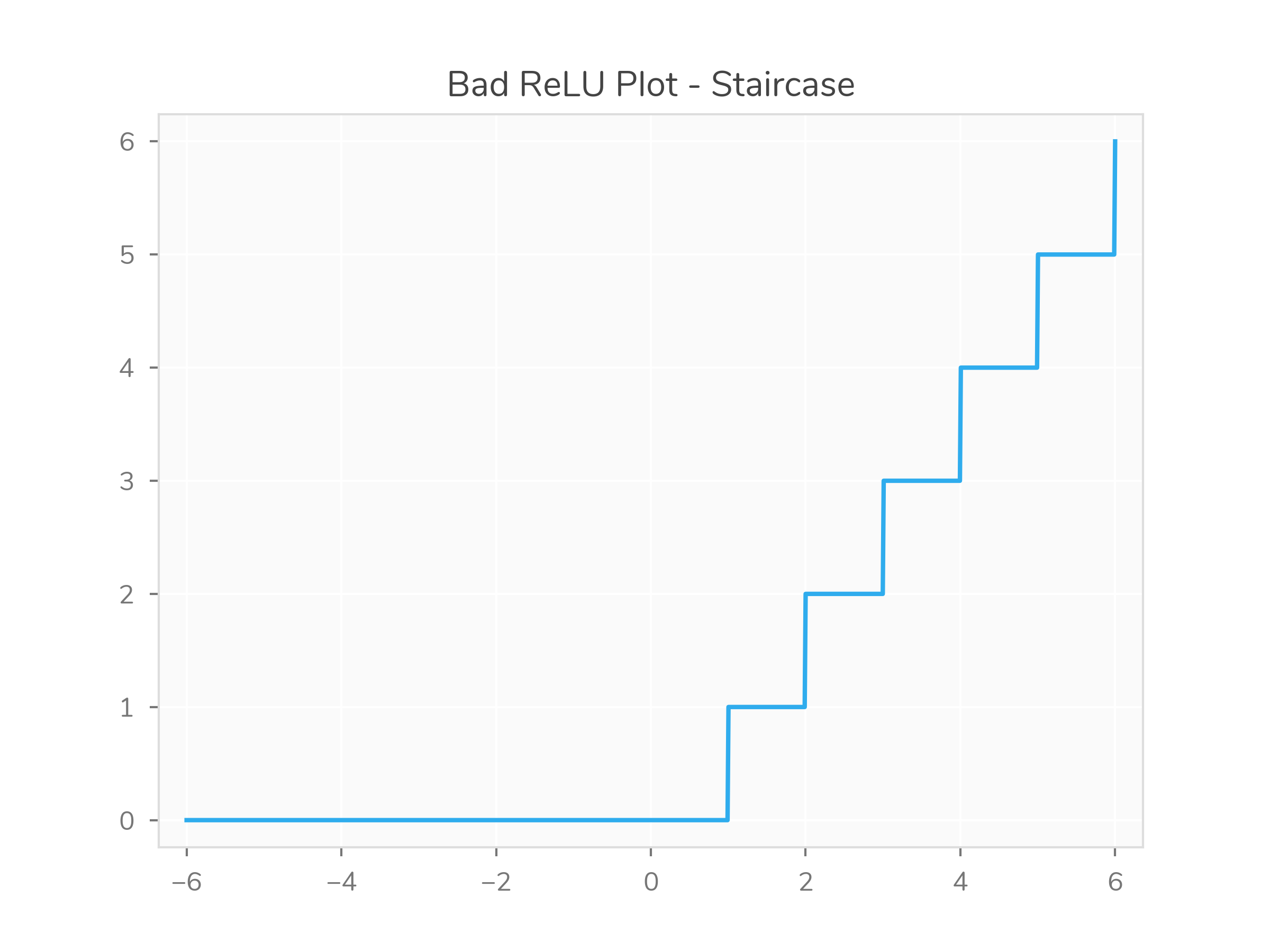
Maybe this hint will help: usingmin(0, x)doesn’t produce a staircase.
This happens because
↩︎max(0, x)is anintfor our firstx, sonp.vectorizeinfers an output type ofint. We can fix this by addingotype=['float']to ournp.vectorizecall, or by using0.0instead of0I can also highly recommend reading this blog post on building type-safe neural networks with dependent types, if you’re interested in this kind of thing.↩︎