Polyrhythms

Polyrhythms are a lot of fun. I might define them as “multiple integer-subdivision rhythms with a greatest common divisor of 1 playing at the same time repeatedly”.

That definition is a little unwieldy though. A simpler casual one could be “playing different numbers of notes in the same amount of time”.

3:2

3:2 or “three against 2” is the simplest possible polyrhythm. (2:1 doesn’t work since 1 divides evenly into 2.)

Here’s me playing a C major scale with 3 notes in the right hand for every 2 in the left.

Another musical example is the second of Chopin’s Trois Nouvelle Études.

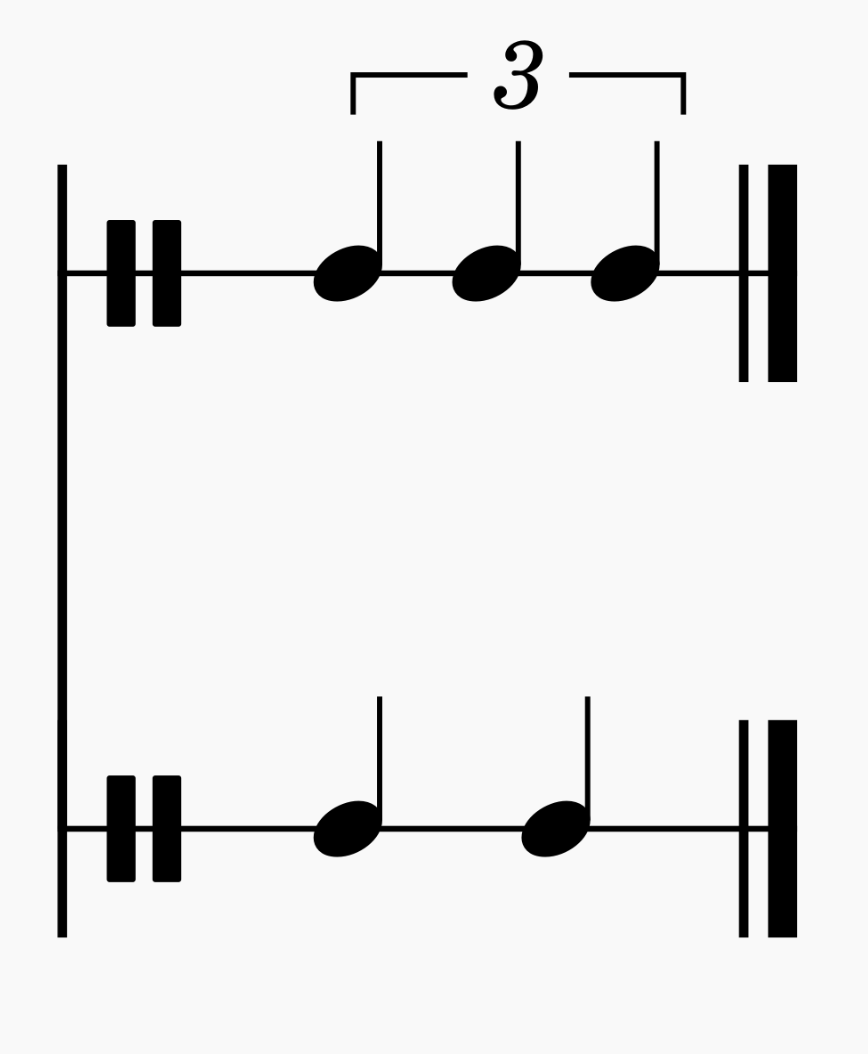
In sheet music notation, we have a triplet over two notes.

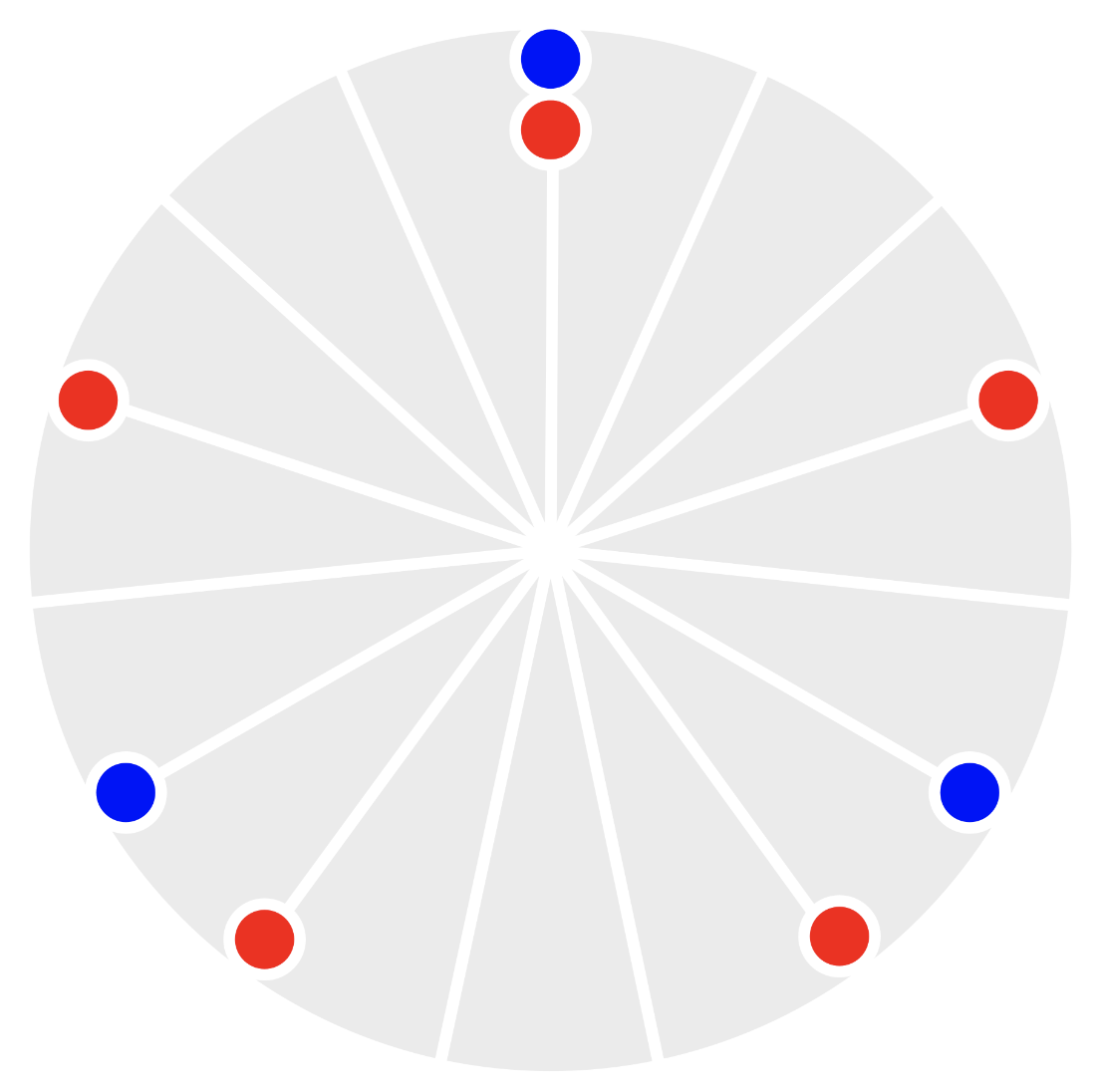
It might be helpful to look at this circular “clock diagram” visualization that shows where the beats line up. It’s divided into 6 pieces since 6 is the least common multiple of 3 and 2.

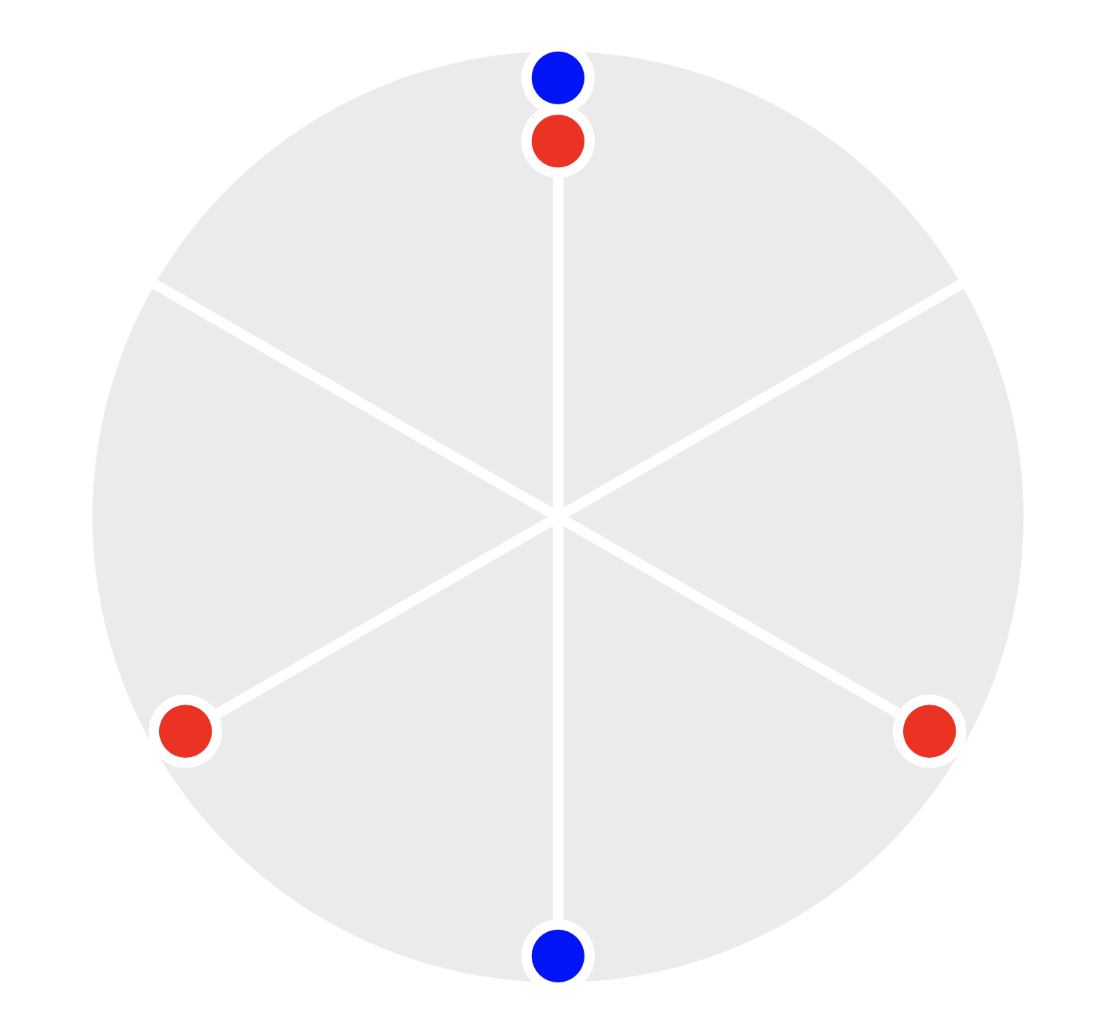
In words we could count: “both, rest, right, left right, rest” at even intervals, and then repeat that pattern.

A polyrhythm’s second number (the denominator) is based on the underlying rhythm of the music. 3:2 and 2:3 sound the same in isolation.

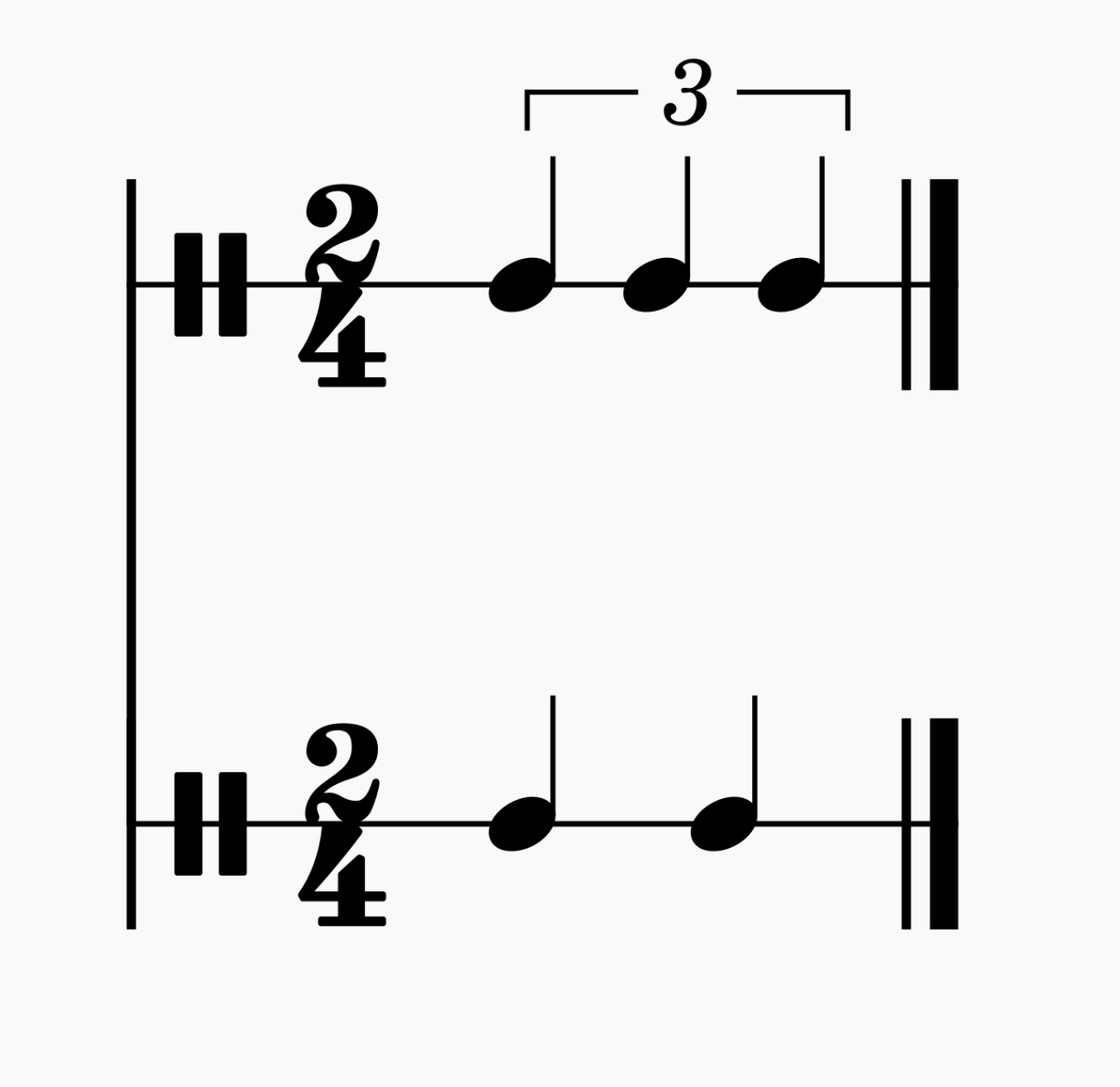
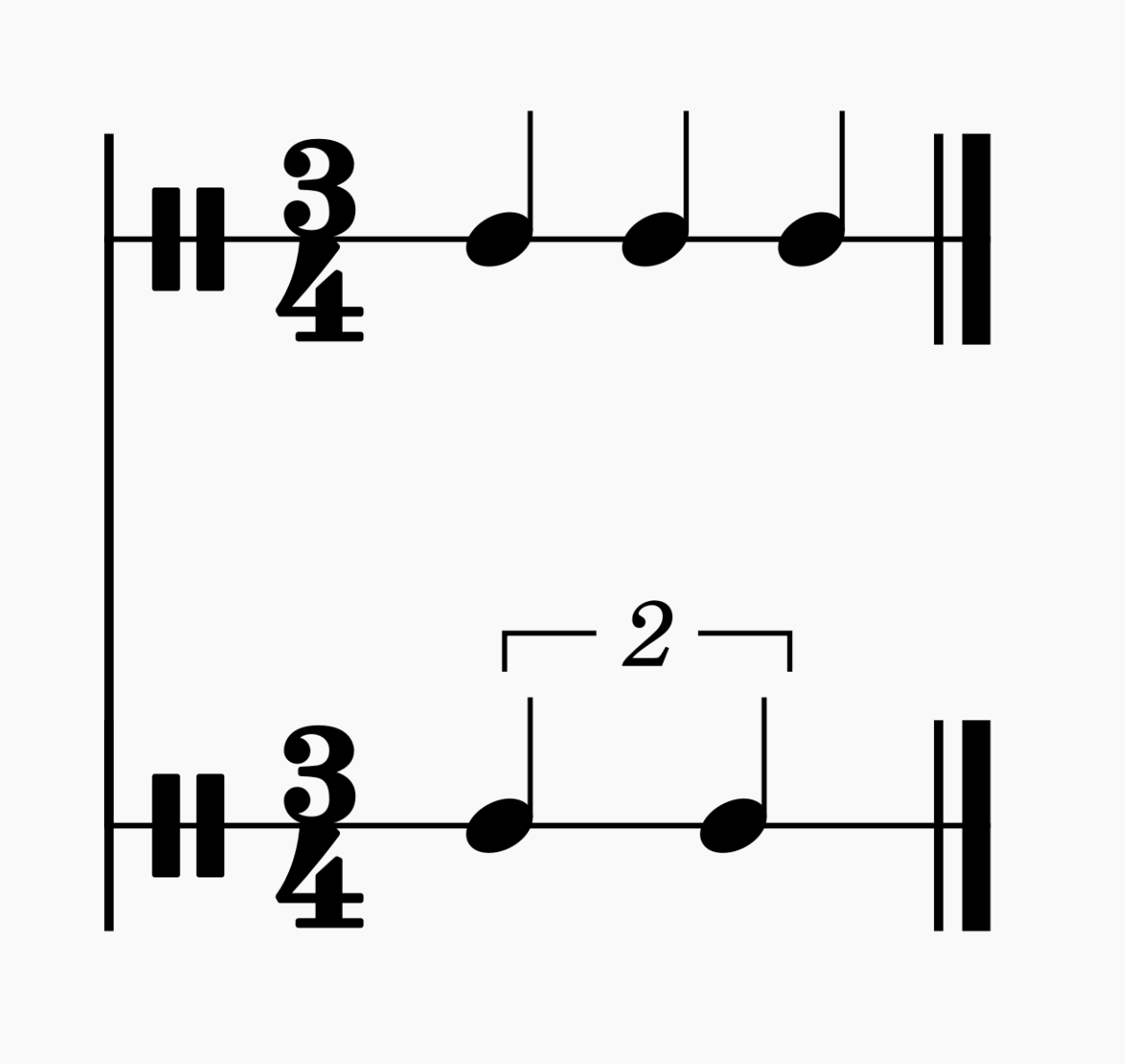
However, in different musical contexts we feel them as different rhythms. 2:3 feels like two dotted quarter notes in 3/4 time, while 3:2 feels like a triplet in 2/4.

4:3

The 4 against 3 C major scale sounds like this:

A famous Chopin example is his Fantaisie Impromptu Op. 66.

As you might expect, we can notate this as four eighth notes over a triplet.

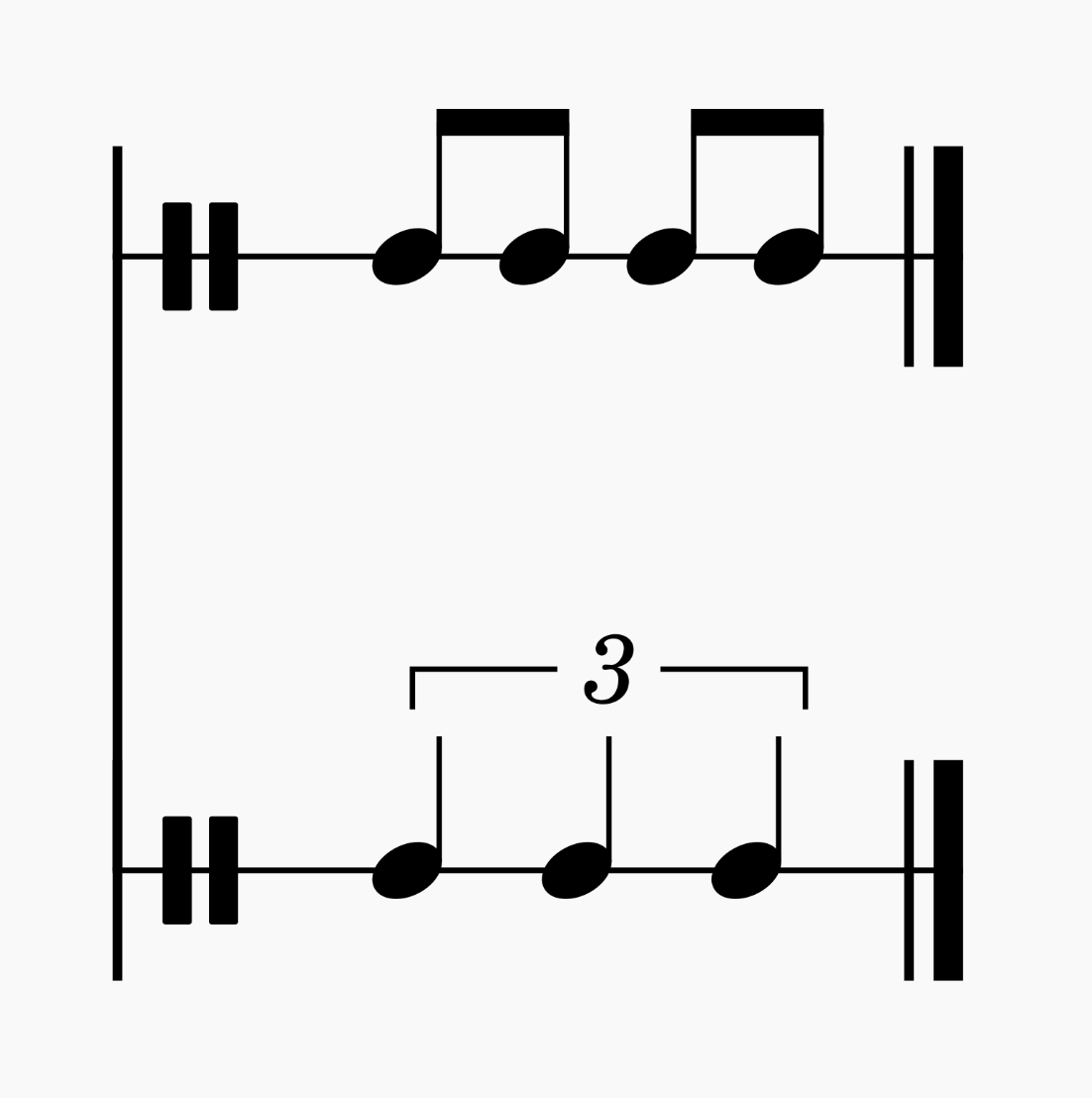
The LCM is now 12. We have to be able to feel different lengths of rest now (1 vs. 2).

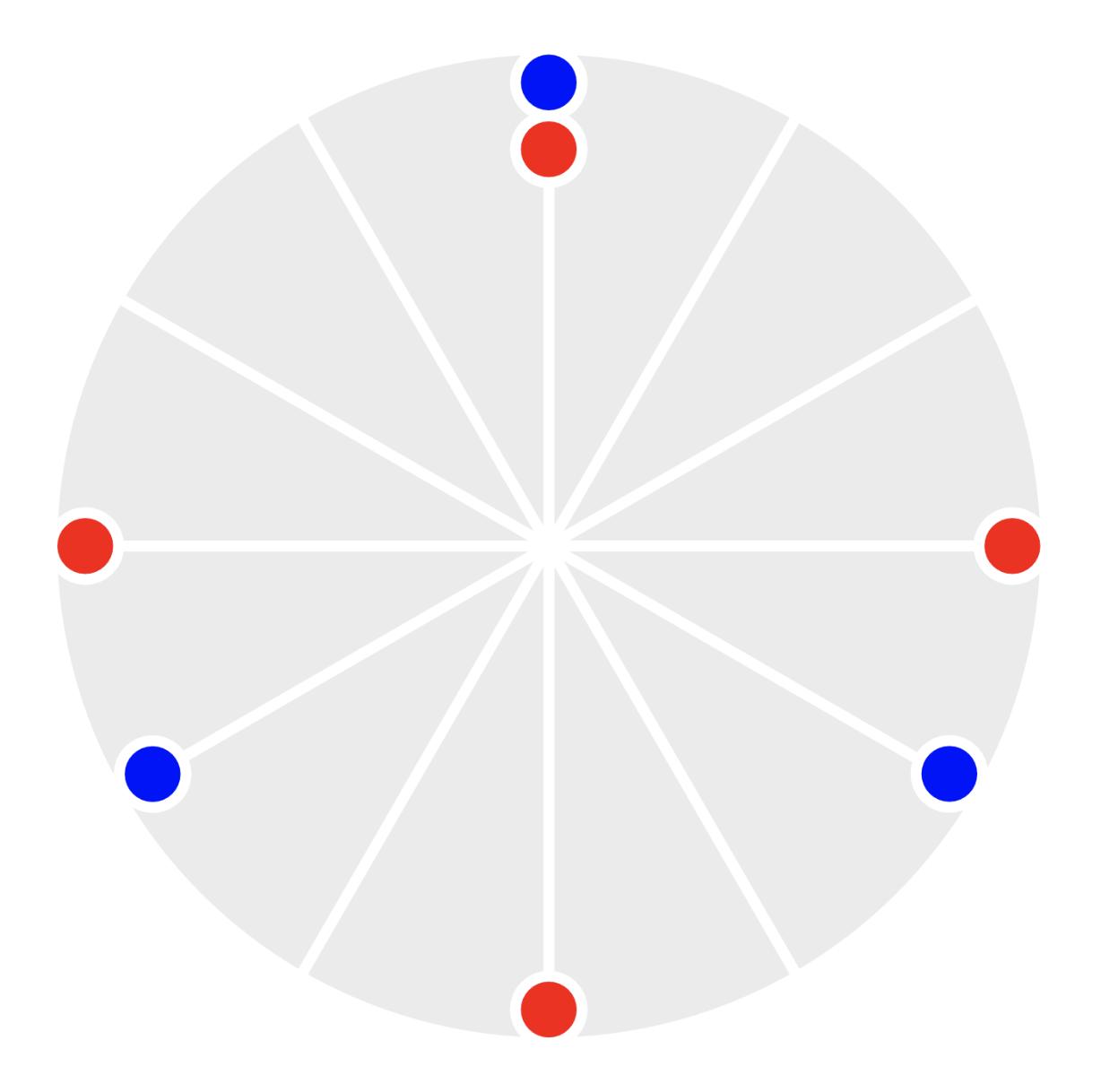
5:4

While there’s a 6:5 in Chopin’s Etude Op. 25 No. 1, I couldn’t find a 5:4 anywhere in his music. I could be wrong though.

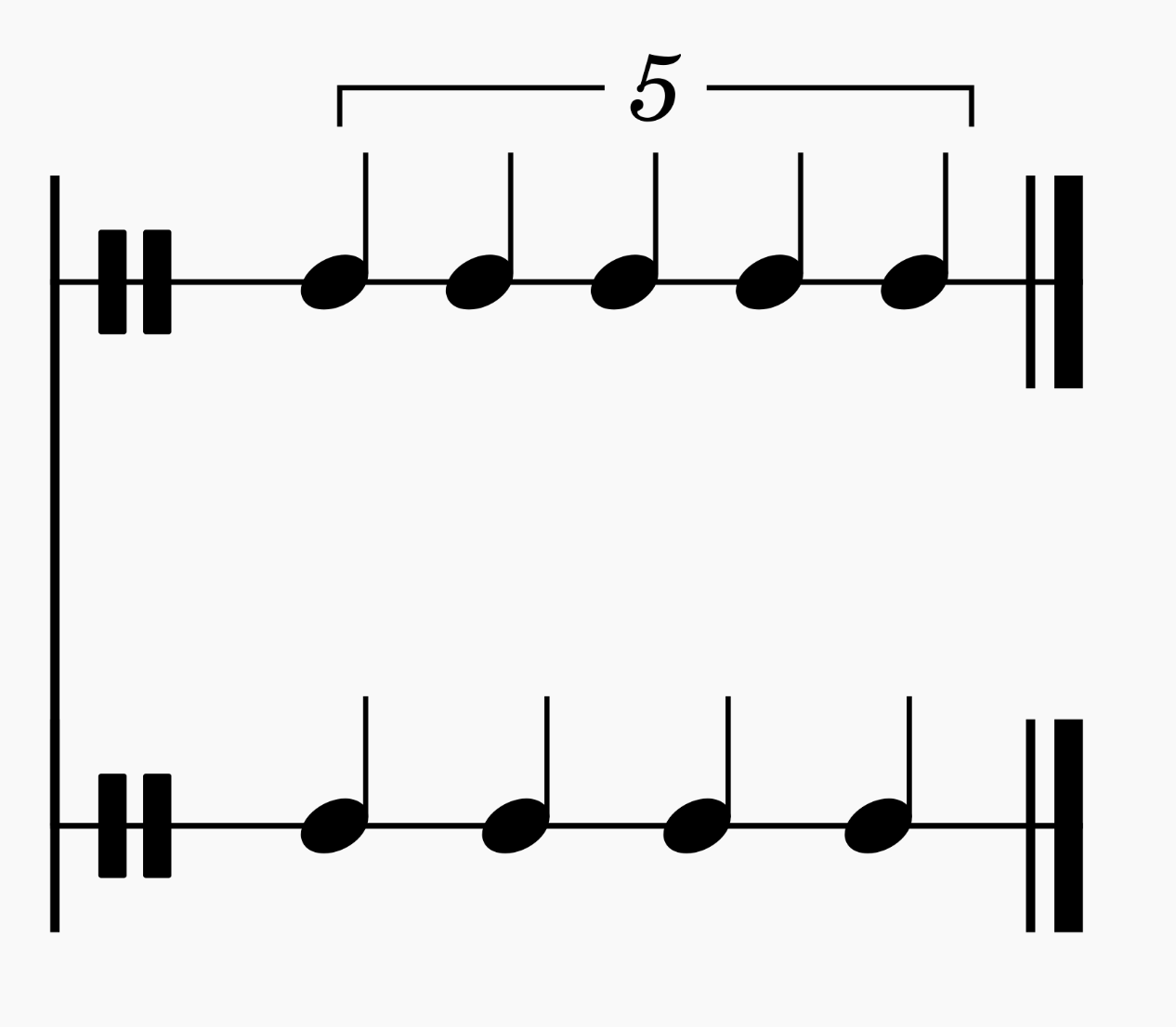
The least common multiple has climbed to 20, and it’s getting pretty hard to feel the rhythm (20 beats per measure is a lot of subdivision).

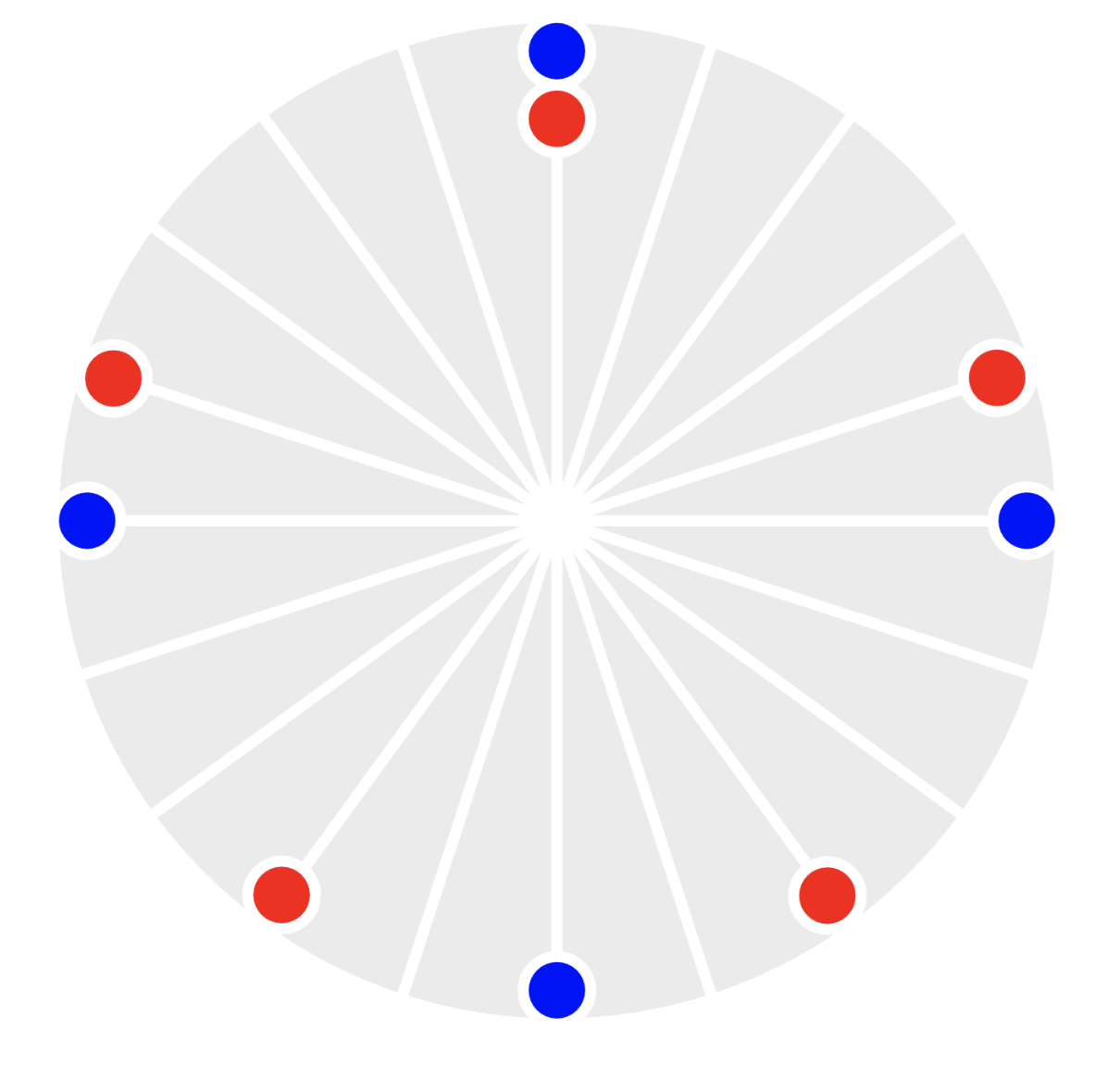
5:3

5:3 is the first polyrhythm made of nonconsecutive numbers.

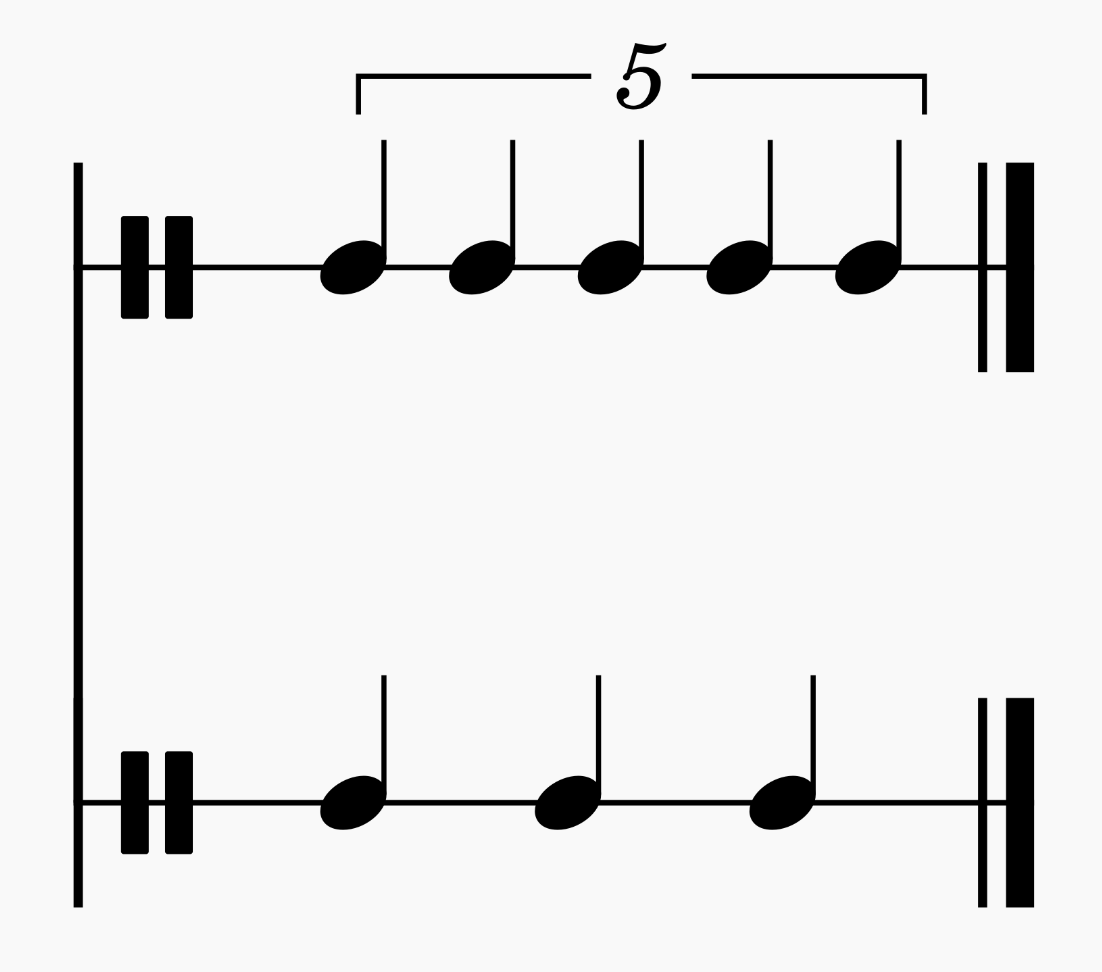
This means it introduces something new—the hands aren’t simply alternating back and forth anymore.

Even higher values

In Chopin’s Nocturne in C Sharp Minor Op. Post., there’s a 35:4. There are also an 11:4 and a 13:4 in the same piece. At this point, with an LCM of 140, it’s less of a polyrhythm and more “just try your best”.

Generating divisions

Because polyrhythms are based on simple math (least common multiple), it’s pretty easy to generate them with a computer.

This code will generate the timings of a polyrhythm described in beats:

import Prelude
import Control.Concurrent (threadDelay)
import Control.Monad (forM_)
import Data.List (intercalate)

beats :: [Int]
beats = [3, 4]

main :: IO ()
main = do
  let denominator = foldr lcm 1 beats
      bpm = 20
      delay = 1_000_000 * 60 `div` bpm `div` denominator

  forM_ (cycle [0..denominator - 1]) $ \i -> do
    putStrLn . intercalate " | " $ map (showBeat denominator i) beats
    threadDelay delay

showBeat :: Int -> Int -> Int -> String
showBeat denominator currentBeat beat =
  if currentBeat `rem` (denominator `div` beat) == 0
  then show beat
  else take (length $ show beat) (cycle " ")

Polyrhythm Rag

Just for fun, I composed a little piano tune full of polyrhythms. It contains 3:2, 3:4, 5:4, 7:4, 9:4, 11:4, and 37:8 polyrhythms (plus a 2:1 at the end, for fun). The repeated note swapping between polyrhythms/hands in measure 4 is interesting, but probably not notated in the best way.

Here’s a computer playing it.