Make Your Own Haskell

I recently gave my first-ever public tech talk, about how to build a Haskell-like language. This is a form of that talk modified to fit in blog post format—not a direct transcription, but hopefully containing the same information. Each slide has its corresponding notes below. You can also download the slides as a PDF.

The core impulse of this talk is the desire to better understand how Haskell works by thinking about how you would make your own Haskell-like language. Because time is limited, it’s mostly a high-level overview of the steps involved.

Of course, implementing Haskell is a huge rabbit hole. So, we’ll pick a language close enough to be recognizably a proto-Haskell, that you could extend in a bunch of ways. The implementation only requires an intermediate (or early intermediate) level of Haskell knowledge—any fancy tricks shown are optional. The language is small enough to be built as a weekend project (realistically, maybe two or three weekends).

Here’s what our language looks like. As you can see, it’s very Haskell-like. We have data constructors, case, let, lambdas. In fact, this is almost runnable Haskell code, except that data declarations only take the number of arguments to a constructor (not their types) and there’s no IO monad so we automatically print out whatever main evaluates to. Also note that there are no type annotations, but the language is typechecked. It’s just that every type is inferred.

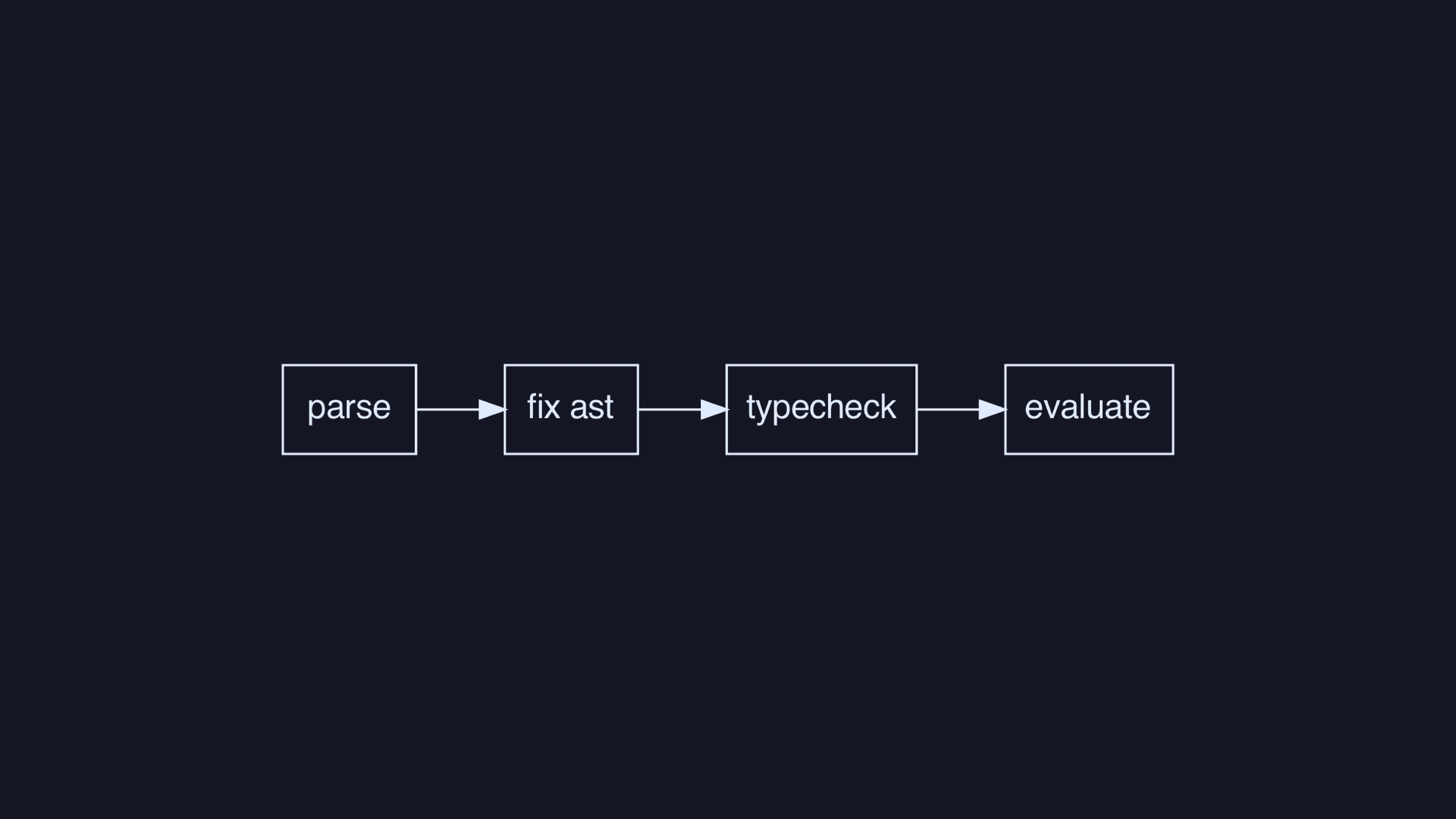
This is the pipeline of steps we’ll need to build to have a working language. The “fix AST” step checks that functions are unique, main exists, and so on. This is all what we’d call “compiler frontend” since we’re not doing code generation (which would be “compiler backend”).

So, this talk isn’t really about Haskell, I’ve sort of tricked you.

Instead, it’s mostly about trees. It involves a bunch of Haskell, but the main thrust of this talk is how we go about dealing with trees, since they’re such a good representation of languages.

Here’s a simple example of an artistic composition. There are roughly two parts: the black part and the gray part. This is an example of the simplest kind of composition: a pair. We use the on operator to join the black and the gray together.

Once we have pairs, it’s a very short step to start building trees. Whenever we’re composing in a nested way, a tree representation makes sense.

In case you don’t believe me about the power of trees, consider this. Trees are so ubiquitous that space itself has a very natural tree representation. There are three directions in Euclidean space: \(x\), \(y\), and \(z\). Octrees divide Euclidean space into eight octants \(((+x, +y, +z), (-x, +y, +z)...)\). Basically, if you have two bits of space next to each other, you can represent the combined larger space by using a tree.

Trees are also great for representing languages, with their structure of nested composition.

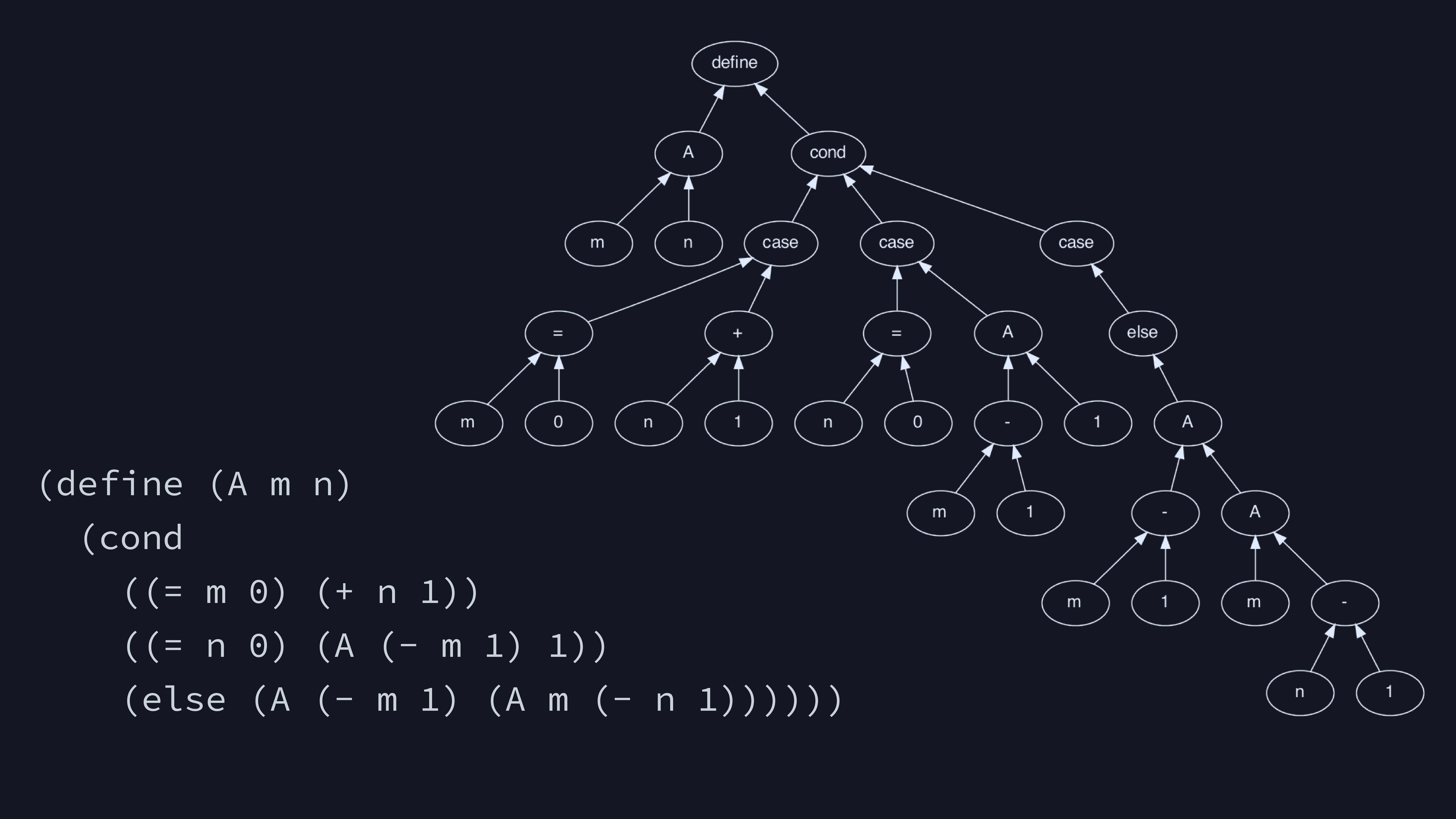
Certain languages represent their own parse trees very directly. Here’s the Ackermann function in Scheme. Once you learn to read the nested parentheses, it’s super straightforward to build the corresponding tree.

Going from Haskell syntax to a parse tree isn’t that simple. However, Haskell (and other ML-family languages) is great to build languages in, since its tree-handling tools are world-class. ADTs give us a compact way to represent well-typed trees. We have pattern matching and exhaustiveness checking so we can handle each possible branch and make sure we don’t forget any. Haskell also has some pretty advanced type system features, to help us really guarantee correctness. Working with trees in Haskell is a great experience.

Let’s actually start building our language.

First, we’ll define some helpful types. A Name is a lowercase name, as in a variable or a function. A Tag is an uppercase name, like a data constructor or a datatype. An Arity is the number of arguments to a data constructor.

A program is just a bunch of top-level functions. (Our language also supports top-level user-defined data declarations, but we’re ignoring those right now for expediency.) One of the functions should be main, but we can just error out if it doesn’t exist.

A function has a name, a list of argument names, and a body expression.

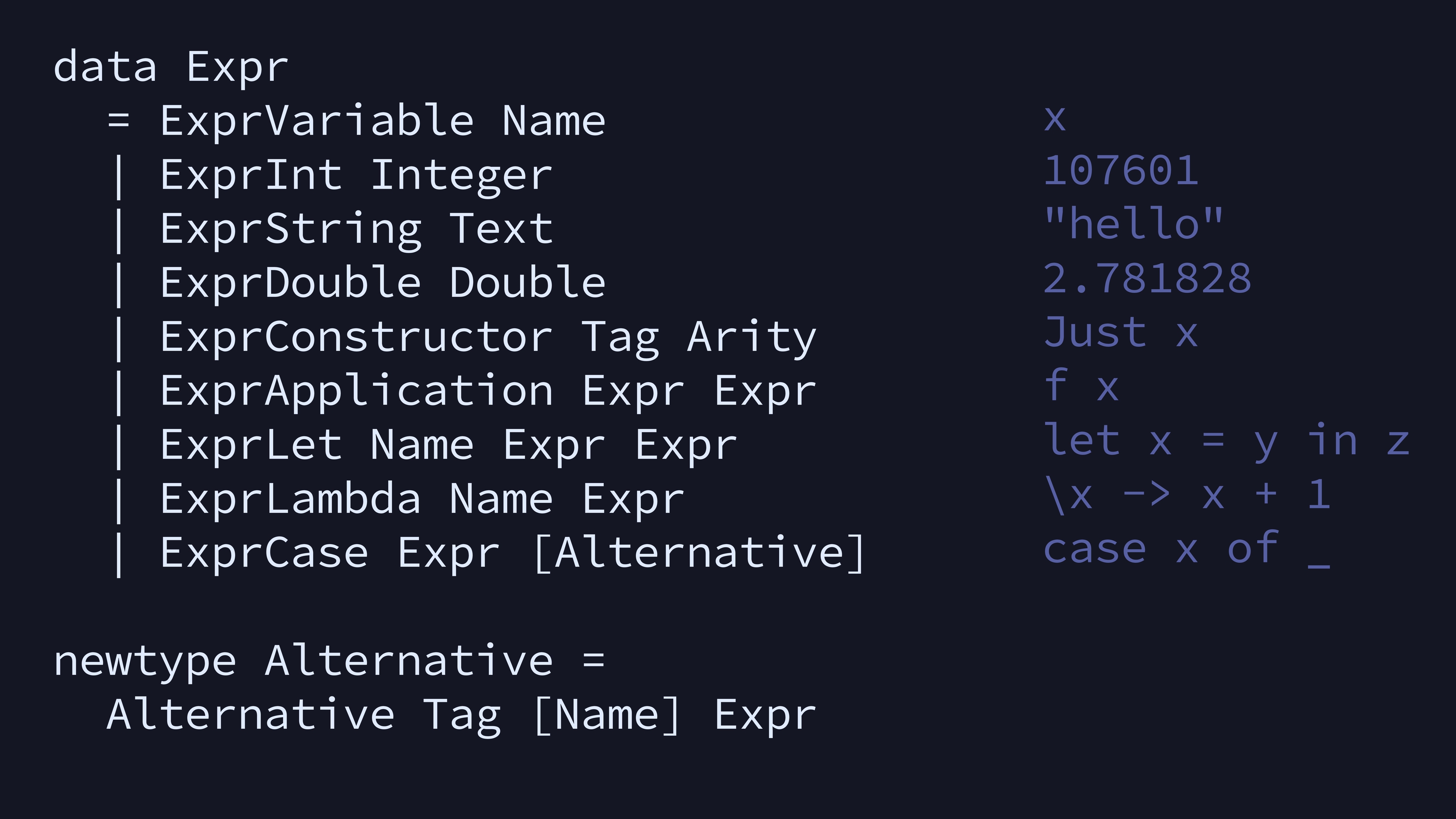
Here’s the meat of our language. We have three kinds of literal—Int, String, and Double. There are no primitive booleans, we use ExprConstructor for that. Note that ExprLet and ExprLambda only allow one argument. To get multiple arguments, we can nest them (as in the equivalence between \x y z -> x + y + z and \x -> \y -> \z -> x + y + z).

There’s a problem that arises when you’re creating a language, of needing many very similar trees. We might want a tree where expressions know their position in the source code, a tree that knows the types of its values, a tree that ignores all this extra stuff and is easy to work with, and so on.

There are a bunch of approaches to decorating ASTs. This blog post outlines some of them pretty well. For example, we could duplicate the tree (but that repeats a lot of work and then we have to keep the two trees in sync somehow). We could add a nullable field to each node (but then you’d have to deal with unwanted nullability in some cases).

My preferred solution is that we can annotate our AST by parameterizing it over some type a.

There’s this paper Trees that Grow that has a lot of insights about working with trees. For example, there’s a way to tack on new constructors to a tree that already exists….

…however, we’ll only use one of its insights. And that’s to use the PatternSynonyms language extension.

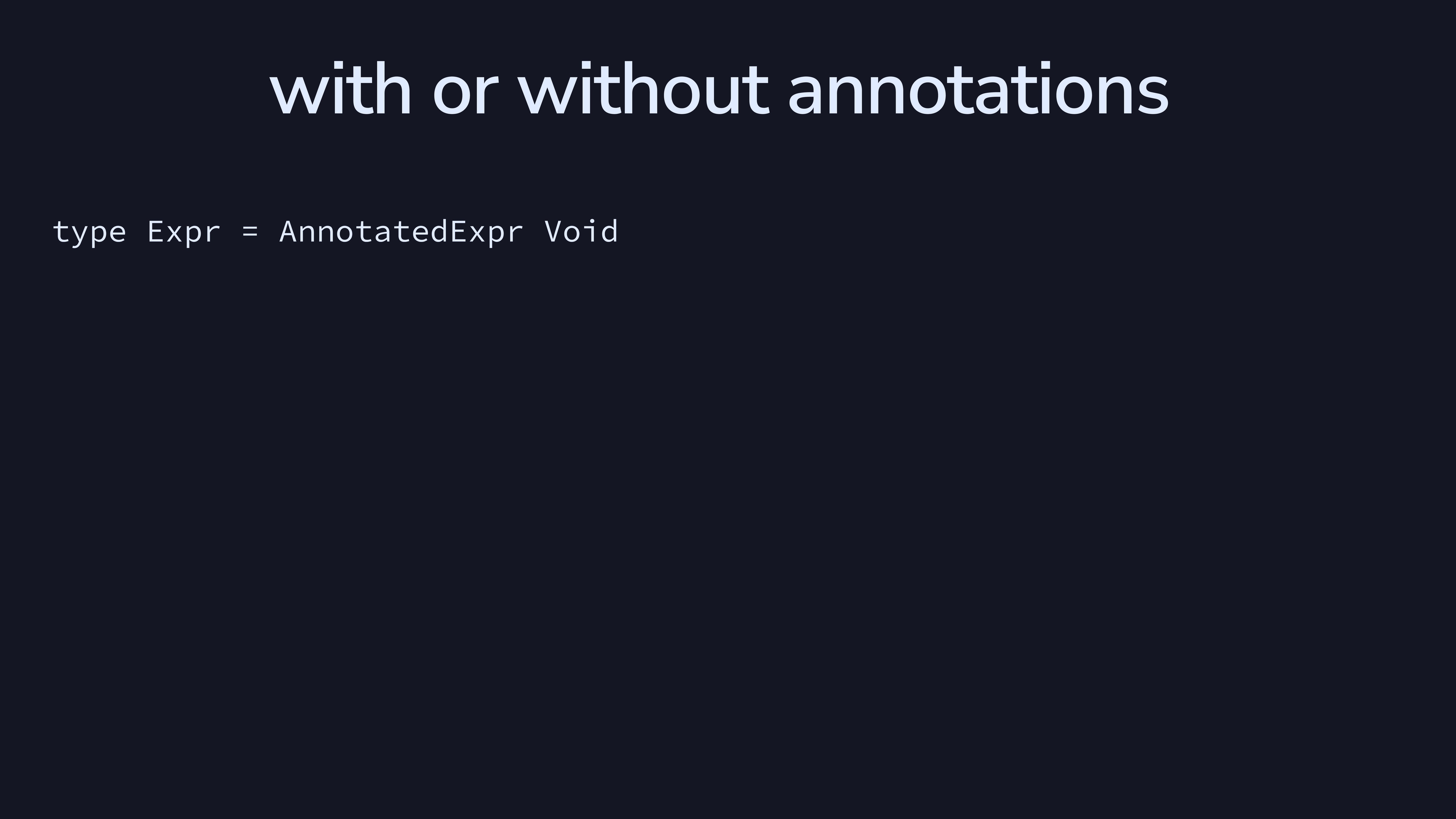
We can find a way to easily work with these trees whether or not they have an annotation attached. First, we define the type synonym Expr to be AnnotatedExpr where the annotation is Void—it doesn’t exist.

Then, we create an explicitly bidirectional pattern match. ExprConstructor is a pattern that matches an AnnotatedExprConstructor but ignores the annotation, and when we use ExprConstructor in an expression, we get back an AnnotatedExpr where void is filled in for us.

We do this for each constructor in our tree.

Now we can use Expr as before, if we don’t care about the annotation, but we can use the annotation when we do care about it. Best of both worlds.

One question I sometimes like to ask people learning Haskell is “what’s the notation for taking the product of \(x\) and \(y\) in middle school algebra?” Because the product is so common, the best notation is no notation at all—we just put the two next to each other. Likewise in Haskell, because function application is so common, we just put the function next to its arguments.

Writing a parser means teaching the computer how to read the notation that we’ve picked.

A parser will have an interface like this. Parser is a monad. Given a parser for a, and some text, this either errors out or gives us the a represented by the text.

As an example, let’s parse the line at the top. SourcePos is the line number and column number of the code we’re currently parsing. The Parser monad can keep track of that for us. We parse the name of the function using parseName. Then, we use the many combinator to parse a list of names for the arguments to the function. We’re glossing over lexing, which you could do as a separate step (breaking your source code into tokens). However, in this case we’ll parse and lex at the same time for simplicity. lexeme basically skips over spaces until we hit the = character, which we parse. Then, we parse the body expression of the function.

Parsers tend to mirror the language itself. For example, a function has arguments and a body, so the function parser has nested parsers for the arguments and the body.

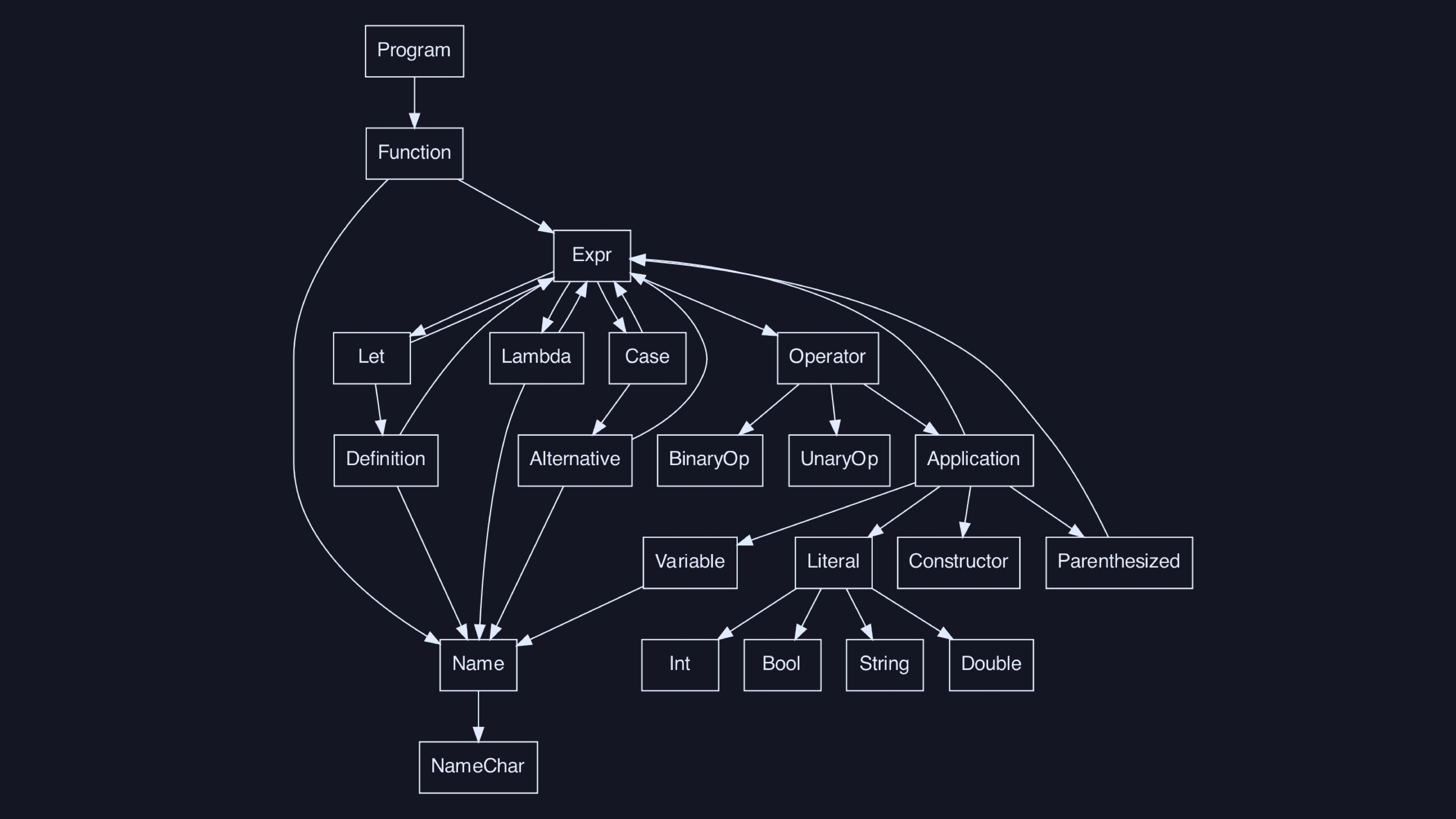
Here’s the call graph of the parsing code for our language. To have a complete parser, we’ll want to write a parseThing :: Parser thing for each thing in this graph. We can unfold this graph into a tree, since it operates on finite amounts of input, so we haven’t left tree-land.

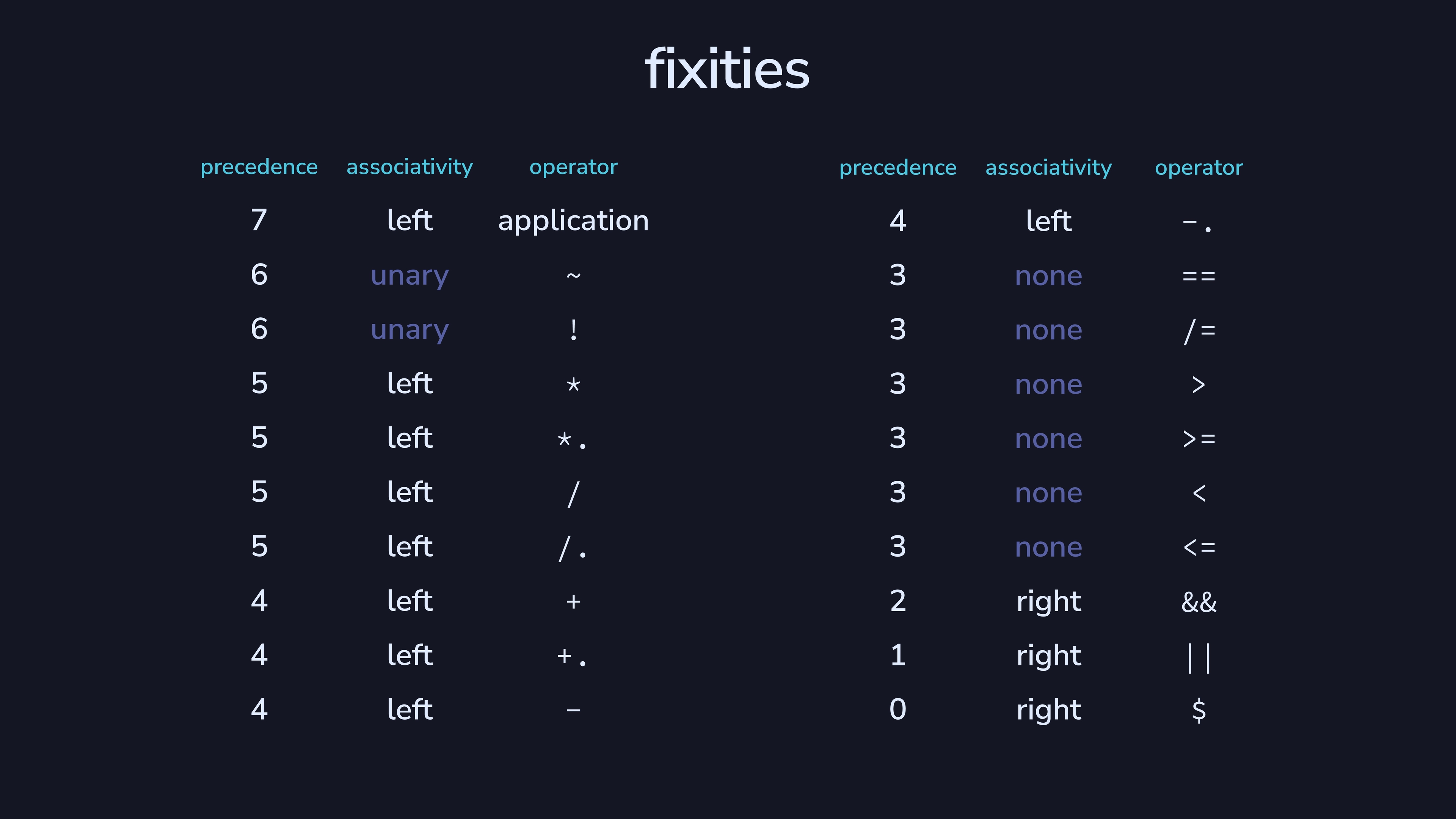
That’s it for basic language features, but we also have 20 primitive operations (score!). In our language, we don’t let users define their own operators. Instead, we bake fixity rules into the language, for simplicity. The function makeExprParser from the parser-combinators library is great for this. You could even use it to let people define their own operators.

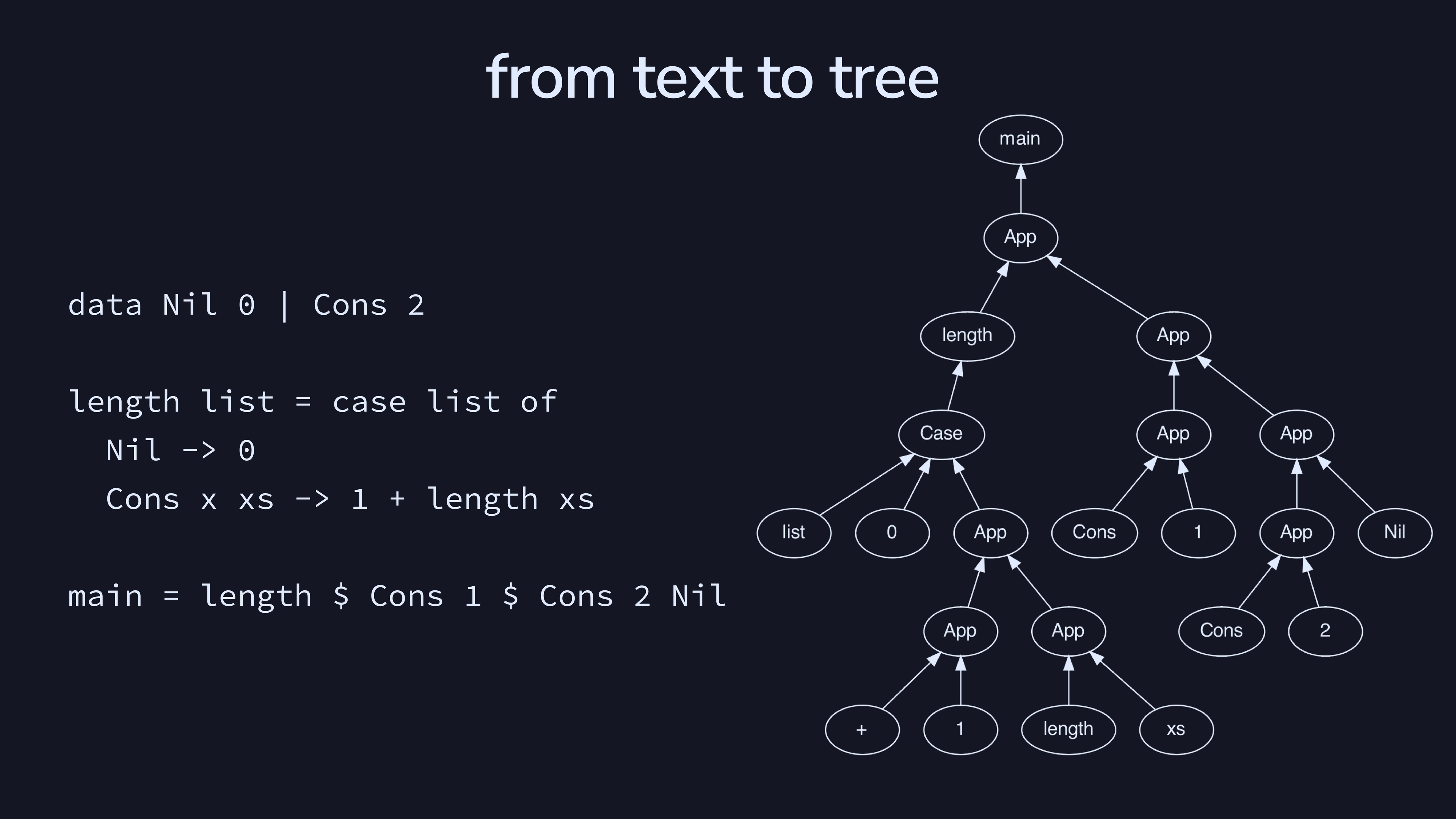
This is an example of parsing a program from text to tree in our language. There are two main branches, which correspond to the call to length and the definition of the list Cons 1 $ Cons 2 $ Nil.

Graphviz is how I made those little “nodes with arrows pointing between them” diagrams. Visual debugging is pretty helpful—it’s much easier to spot what’s going wrong when you can literally see it in front of you, vs. having to reason about a mental model.

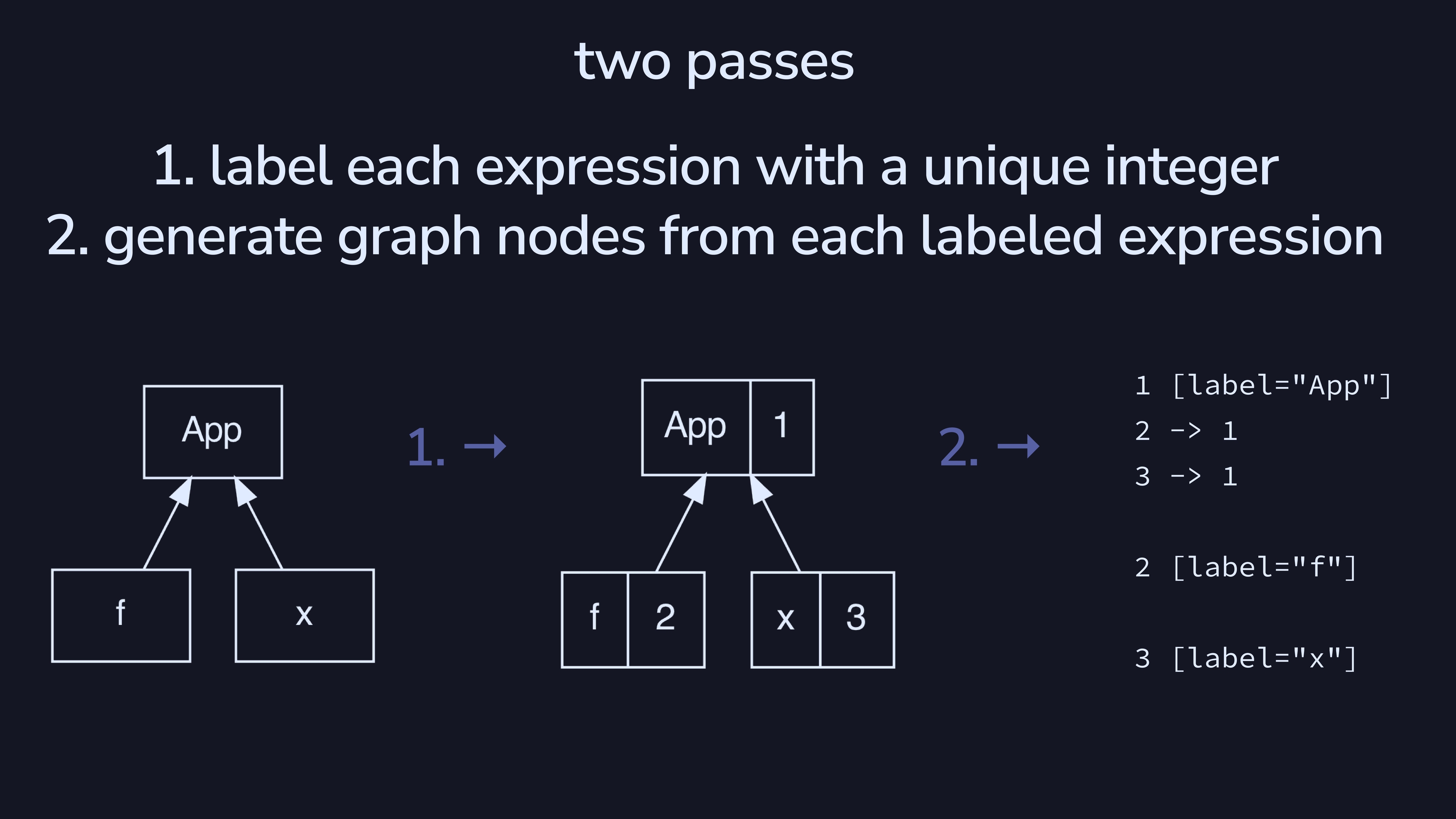
There’s a pretty simple two-pass algorithm for generating graphviz code from a tree. On the left we have a Expr, which we convert to an AnnotatedExpr Integer in the labeling step. Then, we generate code by walking the tree, using those numeric annotations as the graphviz nodes.

In our case, we can build typechecking as a separate pass that we can turn on or off at will. This means we won’t decorate the tree for later use. Instead, we’ll just check that it’s correct.

Each expression has a type. Our three literals each have their own type. Tagged is for the type of a data constructor. For example, the type of False is Tagged (Tag "Bool"). We also allow type variables. Finally, we have a function type which combines two other types (and can be nested to allow longer function types).

Algorithm W is an algorithm that does Hindley-Milner type inference. There are others, like algorithm J, but I wanted this slide to only have a single letter.

This paper has a complete implementation of algorithm W in Haskell. If you’re making your own Haskell, you could just follow along with this paper.

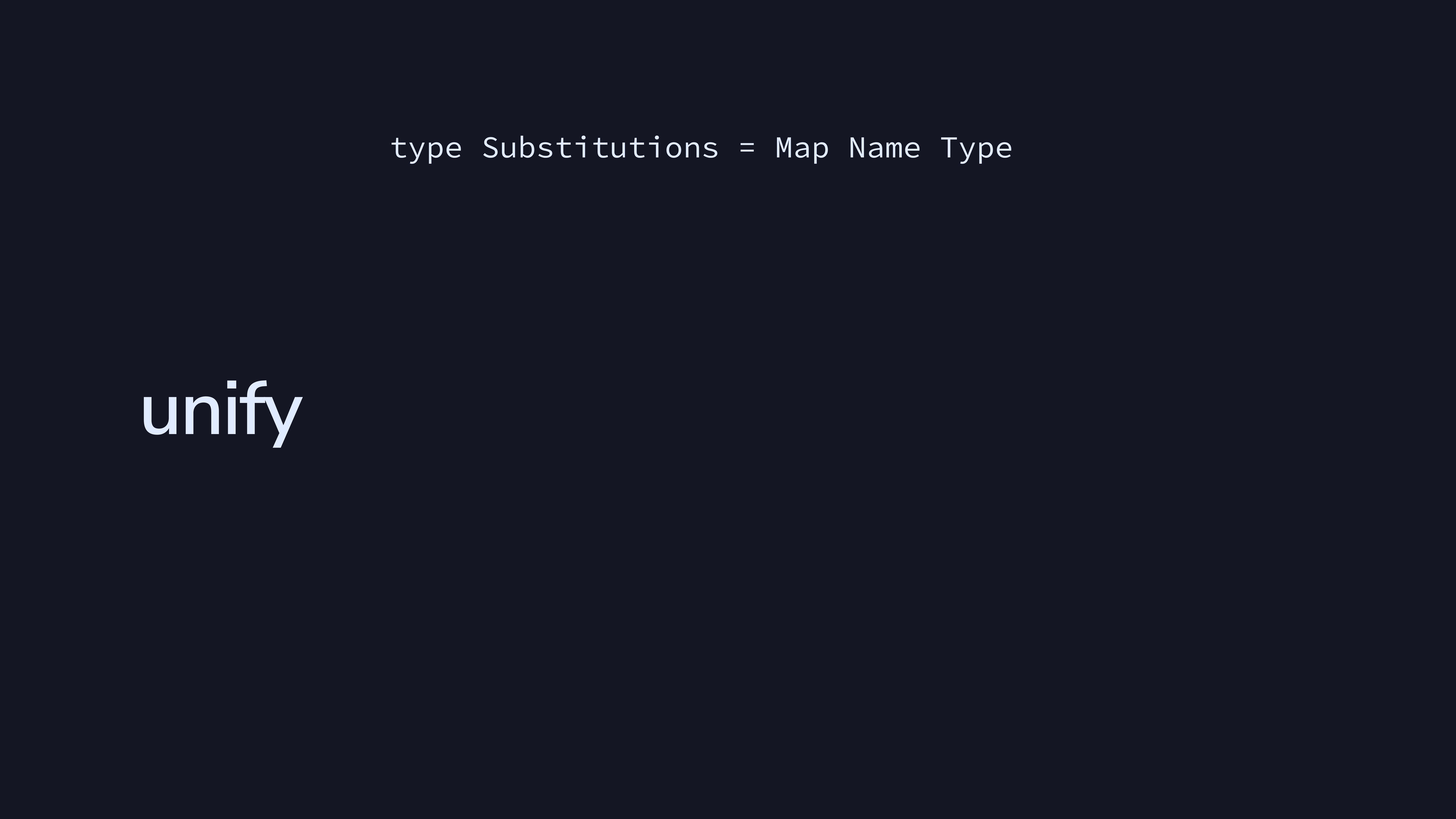
Let’s go over one piece of algorithm W, which is unify. We’ll call Substitutions a map from Names to their corresponding Types.

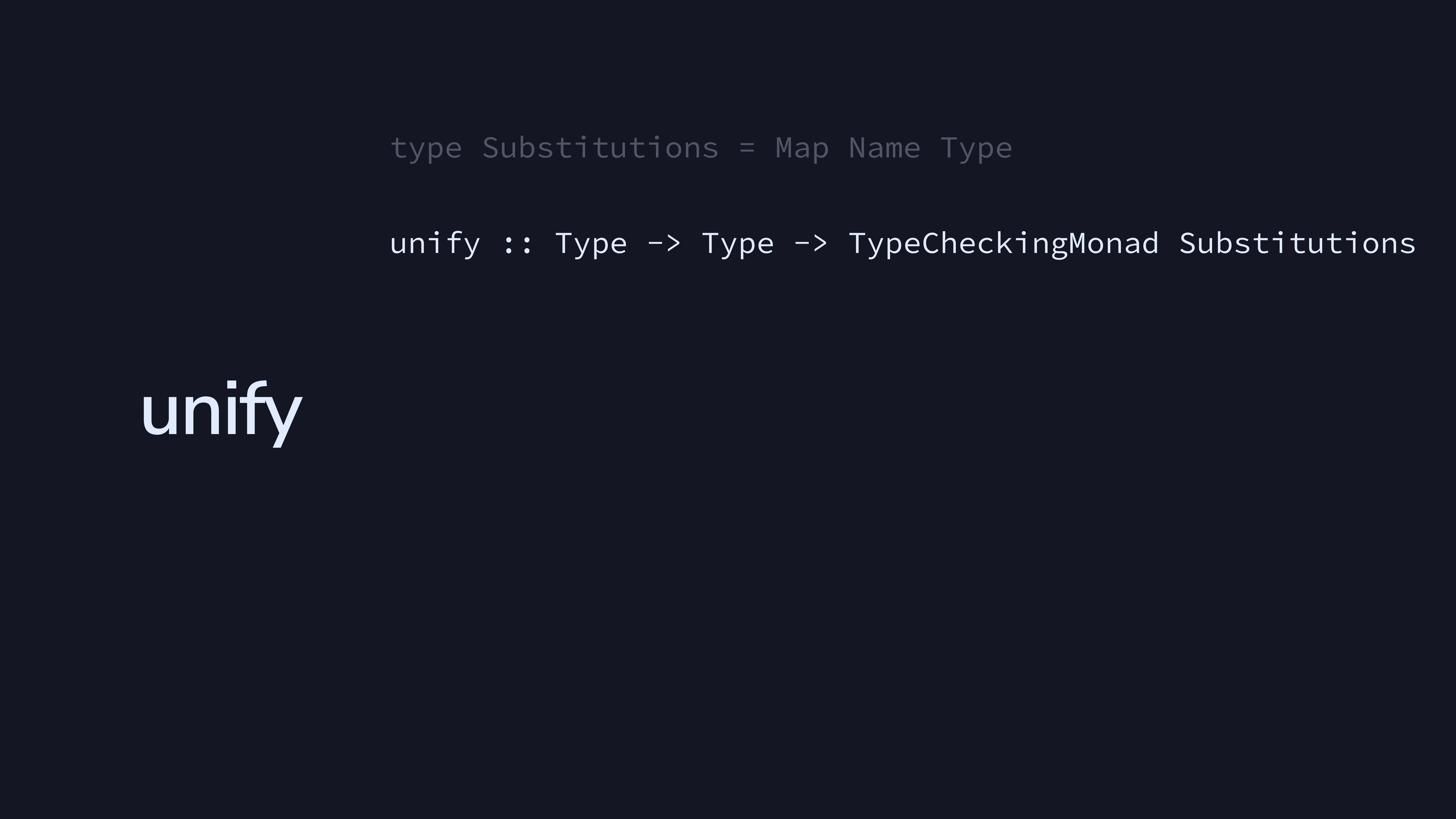
unify takes two Types and checks to see if they match in the context of some TypeCheckingMonad.

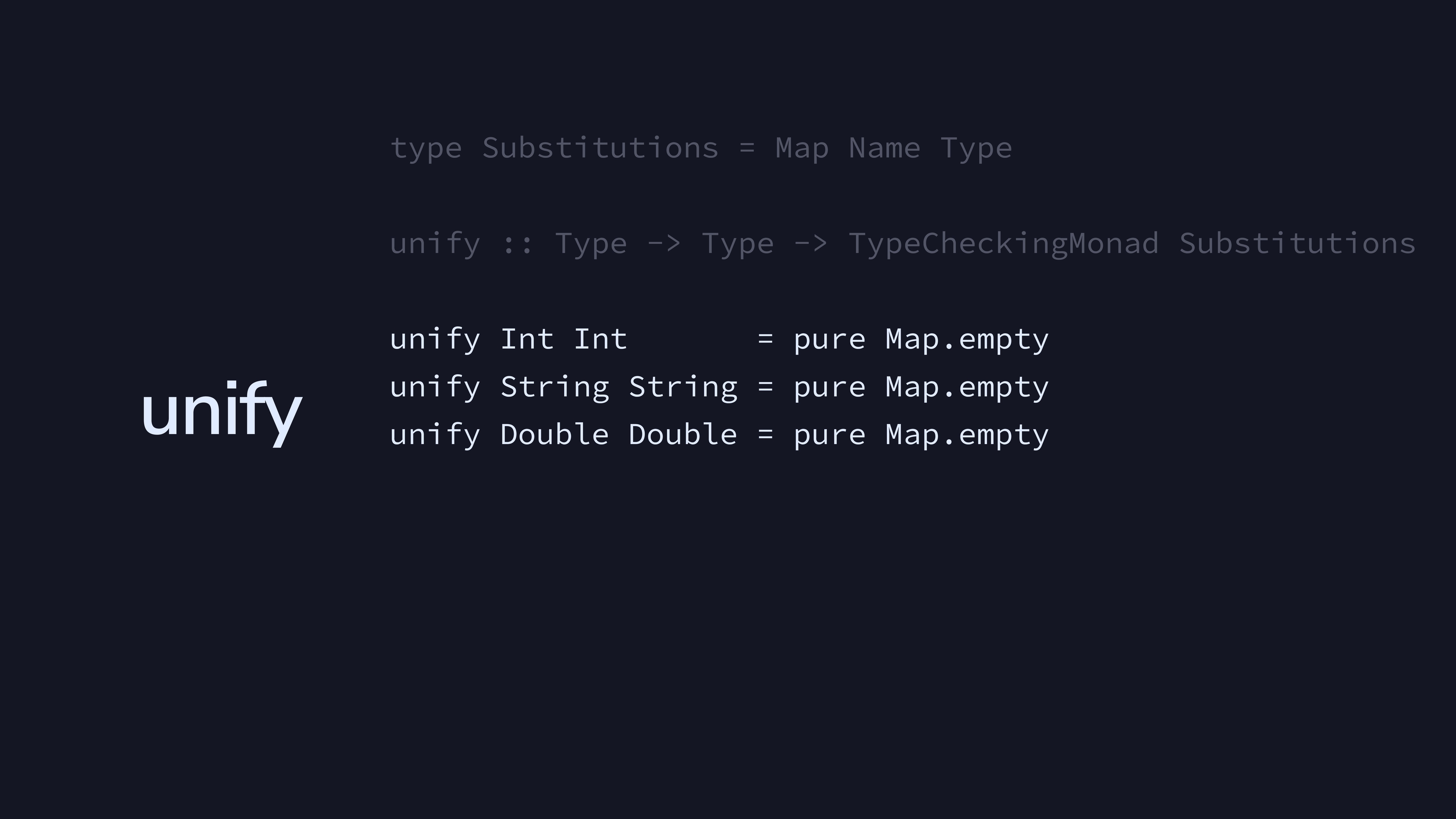
Literals always unify with themselves.

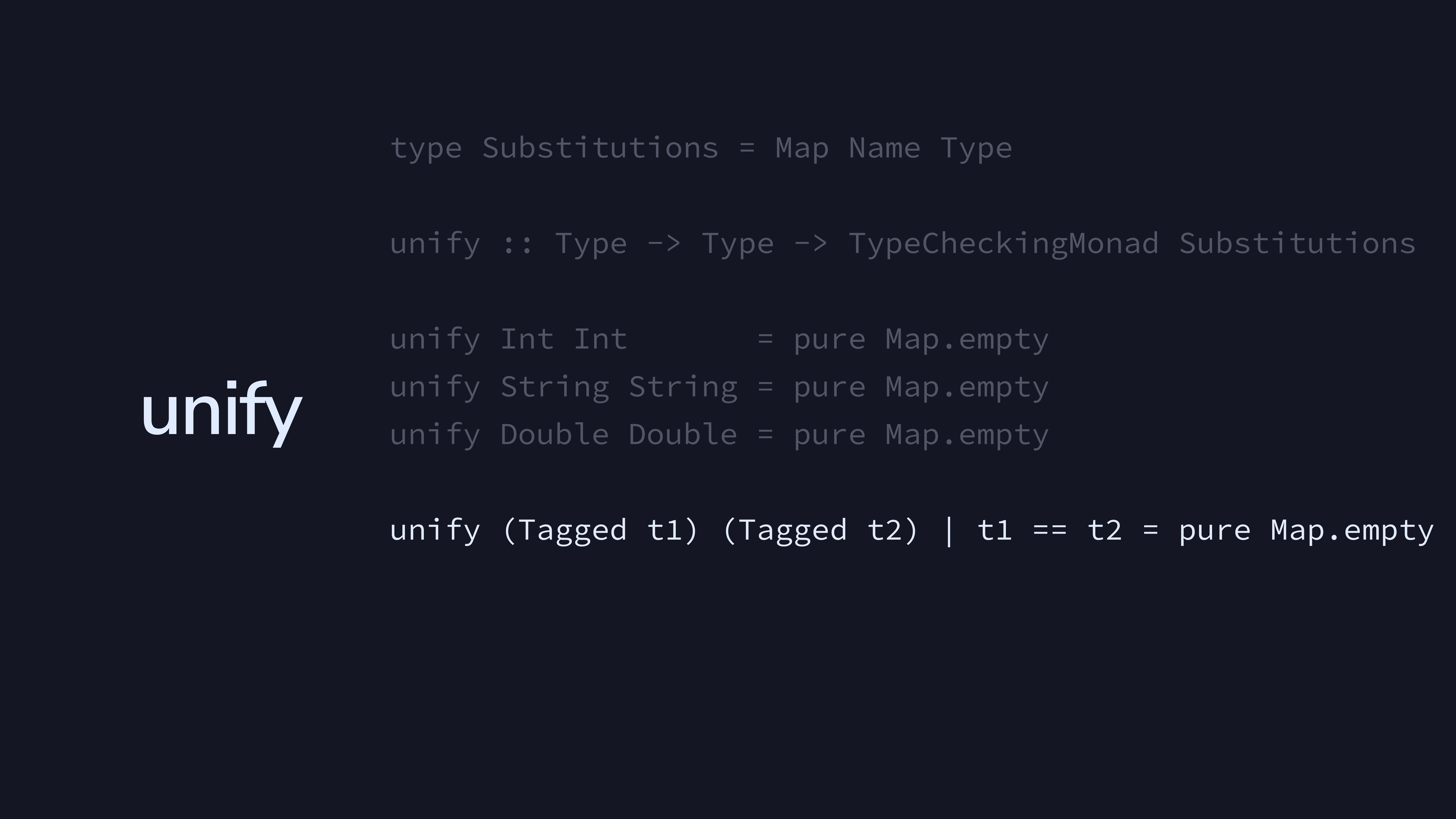
Tagged types unify if the tags are the same. For example, Bool will unify with Bool.

Type variables are a little more complicated. varBind takes a name and a type and either provides a valid new Substitutions map, or throws an exception if var is not in the set of free type variables of t. For more, see the paper mentioned before.

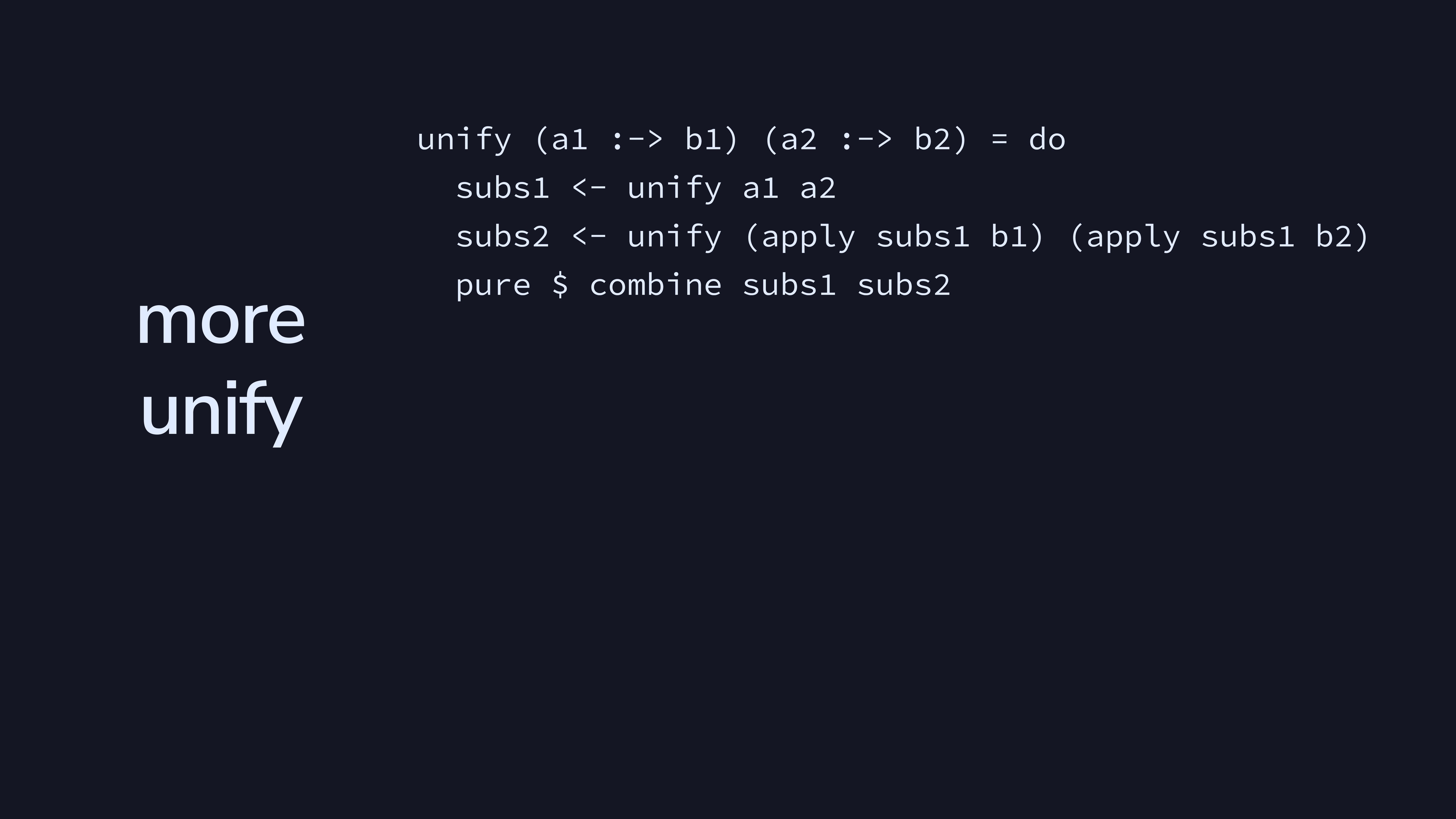
Function types unify if the types of the first arguments unify, and if the types of the second arguments unify in the context of the first arguments. Function types have to have the same number of type arguments to unify, which this checks recursively.

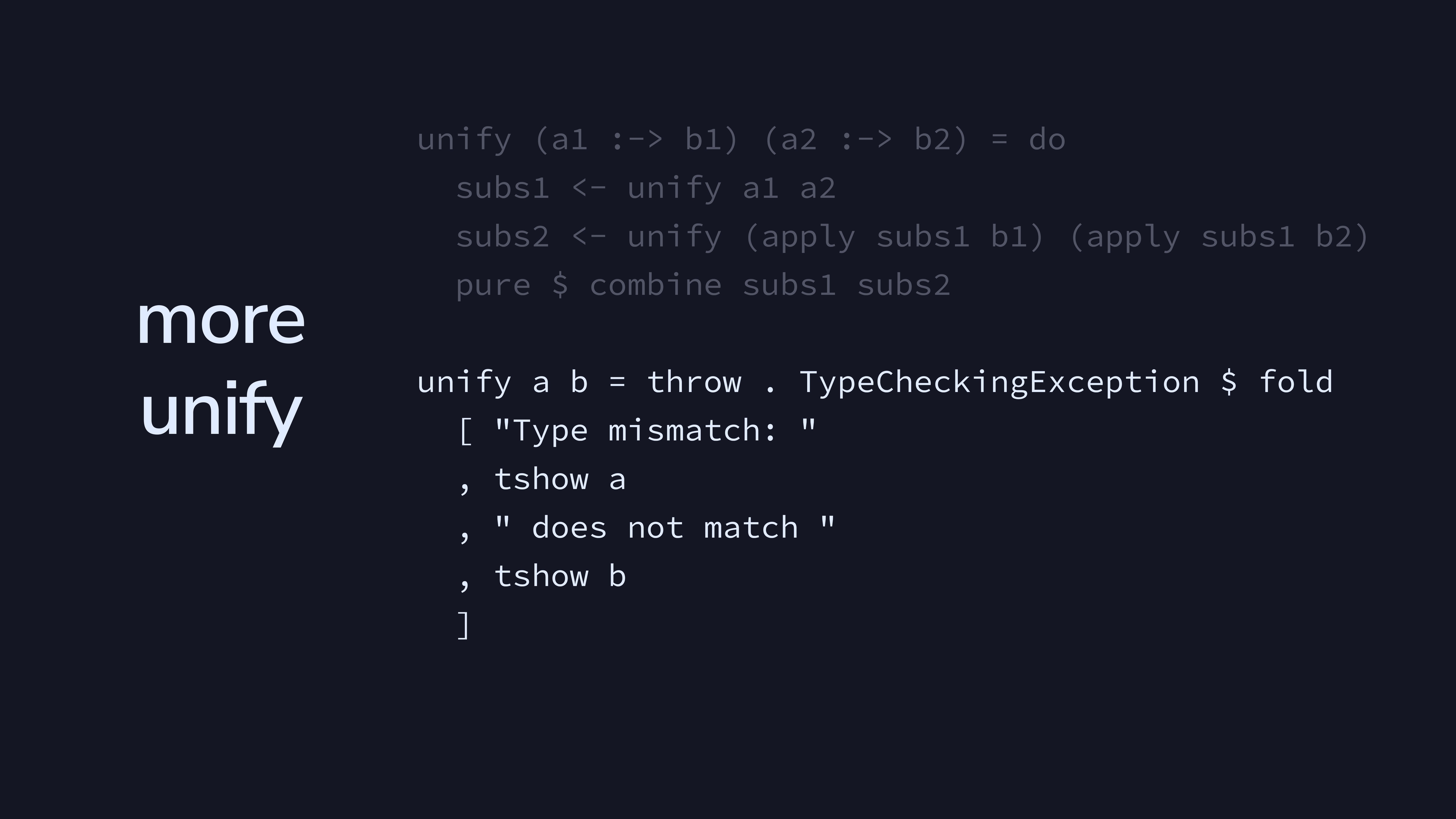
Finally, trying to unify anything else is a type mismatch, which produces a compile-time error for our language.

There are two requirements if you want to have a programming language. You need a language, but you also need that language to be runnable. If we wanted to be fancy, we could call these two “denotation” and “operation”.

The fancy word for this is compilation. However, this talk doesn’t get into STG or Cmm or LLVM or anything like that.

Instead, we’ll just evaluate the tree.

To do that, we’ll write the eval function. It simplifies the expression representing the entire program down to the final value returned by that program. We can then just print that value.

There’s a problem here, but luckily it’s pretty easy to solve. We have a program, which is a collection of top-level functions. However, eval takes a single expression. To fix this, we just combine our functions into a massive let where we let those functions be defined in the body of main.

There’s another problem, which is far more horrifying. Trees are no longer sufficient! Here we have an example where f calls g and g calls f, which is a loop. That means we have a graph instead of a tree. However, it’s even worse than that! f calls itself twice. This means the call graph is a multigraph, not a tree.

To deal with this, we can put variables in an environment of type Map Name Expr so we can look them up as needed. Our new eval will then evaluate an expression in the context of that stateful environment.

If you’re interested in much more depth on compiling lazy functional languages, this book is good. I’d also recommend reading about STG (the Spineless Tagless G-machine) to learn how actual Haskell works.

Let’s evaluate our tree. This will be the most code-heavy part of the talk.

Literals evaluate to themselves. The surprising ones here are probably the bottom two. This is because we evaluate Lambda as part of Application, and Constructor when evaluating Case.

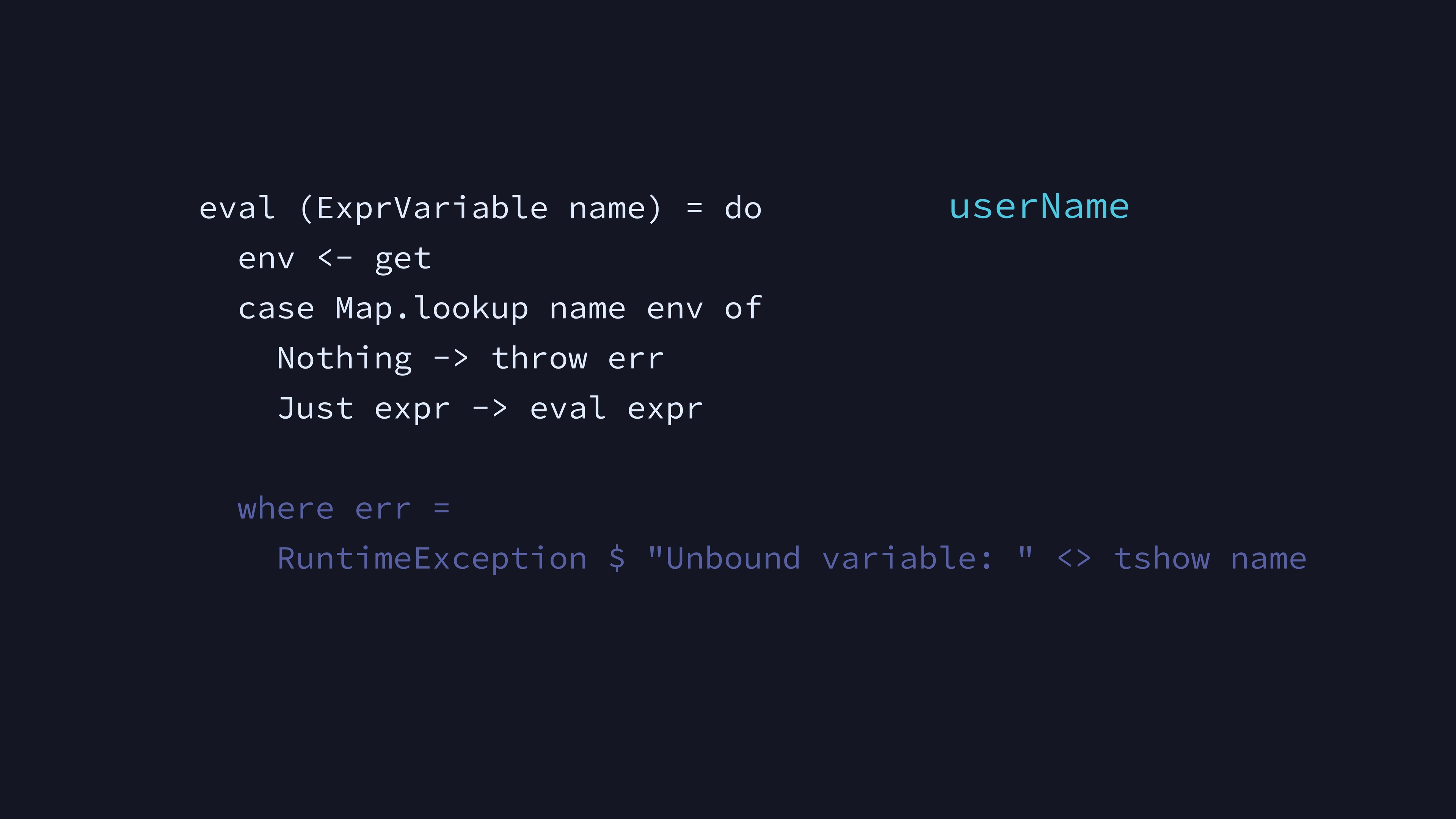
We evaluate a Variable by looking up its expression in the environment, and evaluating that expression. If the name is not found, that’s a runtime exception.

We evaluate a Let by adding its binding to the environment unevaluated, then evaluating the body. It’s important to not evaluate the binding up front—this makes Let non-strict because variables aren’t evaluated until they’re actually used. While our language isn’t actually lazy, this helps recover some of that Haskelly non-strict behavior you can see in the example, where we define x in terms of y which itself hasn’t been defined yet. This also automatically handles name shadowing for us, since we overwrite names in the environment in definition order.

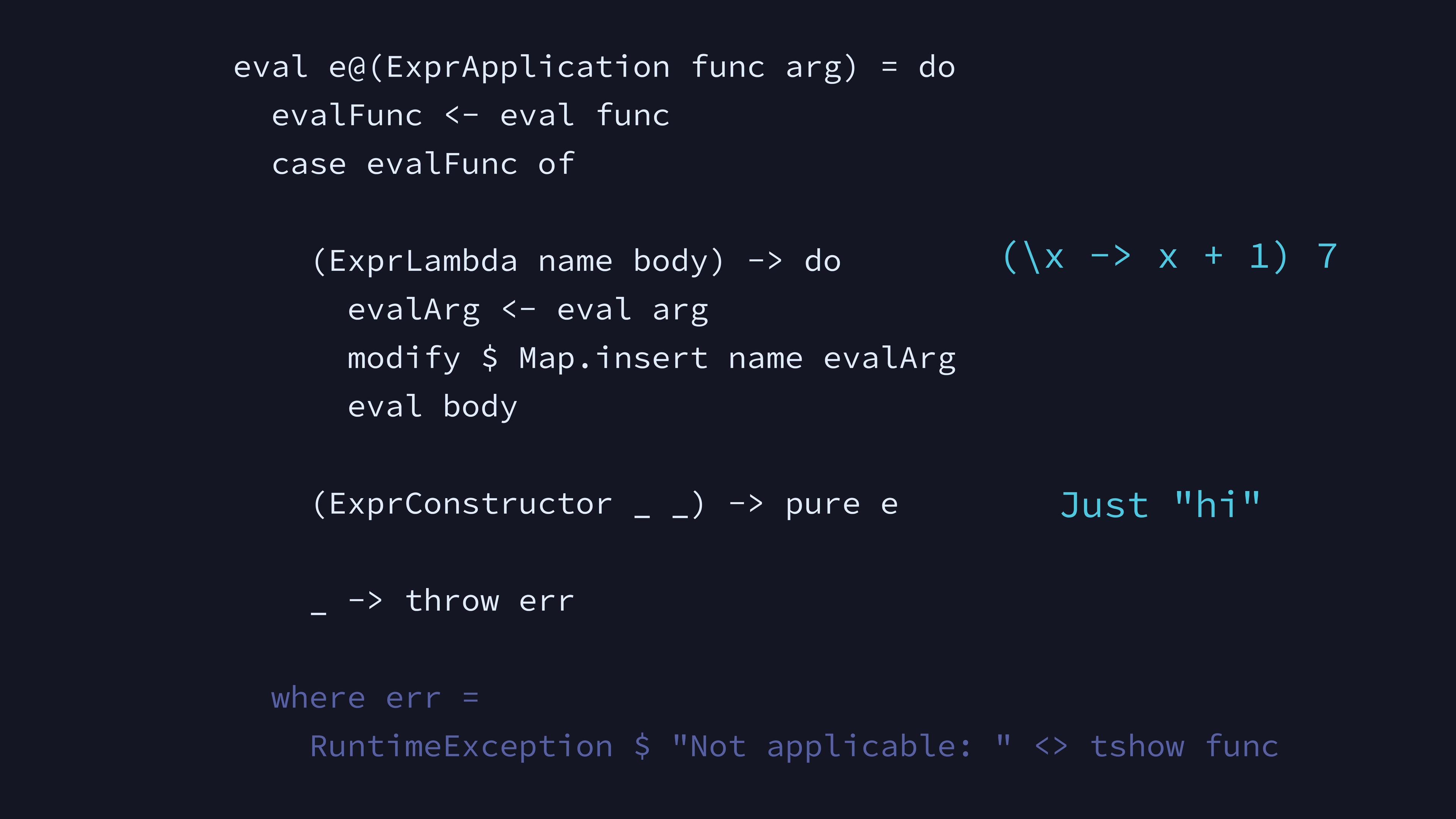
Applying a Lambda works a lot like the Let expression, where we bind a name to some expression in the environment, and evaluate the body expression in that new context. We don’t do anything here to apply constructors, since they’re deconstructed in the case expression.

To evaluate a Case expression, we find the first alternative the scrutinee’s tag matches. We then unpack the arguments to the data constructor (if any), put those arguments in the environment, and evaluate the alternative’s body.

eval will now work for any Expr in our tree, but we can add primitives by adding more pattern matches and defining their behavior directly.

So, in conclusion…

We made a reasonably Haskelly language, but didn’t talk about optimization or code generation at all. There are plenty of improvements still left to make.

Thanks so much for listening reading!